Эмпирической линией регрессии у на х называется ломаная с вершинами в точках с координатами

.

Аналогично определяется эмпирическая линия регрессии у на х – ломаная с вершинами в точках с координатами

.

При этом и - групповые средние, которые определяются для каждого значения x признака X в первом случае и для каждого значения y признака Y во втором. Их расчетные формулы таковы:

, .

3. Коэффициент линейной корреляции r позволяет определить форму корреляционной зависимости. Он подсчитывается по формуле:

.

Средние квадратические отклонения группировочных признаков определяются как арифметические квадратные корни из дисперсий. Дисперсии рассчитываются по определению или по формуле разностей (см. задачу 4), а также методом моментов (см. задачу 5). Величина μ может быть найдена двумя способами: по определению

,

,

а средние арифметические и 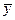находятся по определению (задача 4) или методом моментов (задача 5); методом моментов (см. задачу 5)

.

В зависимости от r имеем следующую интерпретацию связи

Значение r	Интерпретация связи
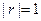
	Линейная функциональная
	Линейная обратная
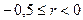
	Нелинейная
	Нелинейная
	Линейная прямая
	Отсутствует

4. Степень тесноты корреляционной связи устанавливается с помощью корреляционного отношения η, равного

,

При этом и - соответственно межгрупповое и общее средние квадратические отклонения, равные

, ,

.

Характер связи определяется так:

Значение η	Характер связи
	Отсутствует
	Практически отсутствует
	Слабая
	Умеренная
	Сильная
	Функциональная

Для проверки правильности произведенных вычислений удобно использовать свойство корреляционного отношения:

.

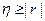5. Проверить гипотезу о статистической значимости эмпирических данных, а следовательно о принципиальной возможности построения уравнения регрессионной модели можно с помощью t - критерия Стьюдента.

Правило проверки гипотезы. Если наблюдаемое значение критерия больше критического,

,

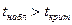То это с вероятностью γ (уровнем значимости α = 1- γ ) говорит о значимости коэффициента линейной корреляции, а следовательно о статистической значимости эмпирических данных. При этом

,

а критическое значение определяется по таблице (см. таблицу 3 Приложения):

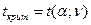, α = 1- γ, ν = n – 2.

Нахождение параметров уравнений линий регрессии у на х и х на у производится путем решения соответствующих систем нормальных уравнений. Для линейного случая существует еще один, упрощенный способ. Вид уравнений линейной, параболической и показательной регрессий и способы расчета их параметров помещены в таблицу 10.

7. Точность построенной регрессионной модели определяется с помощью средней ошибки аппроксимации 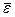, равной

,

при этом y и y* - соответственно эмпирическое и теоретическое (рассчитанное по модели) значение признака Y, соответствующее данному значению x признака X.

Date: 2016-05-25; view: 476; Нарушение авторских прав