
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Если для факторных признаков это условие нарушается, то один из них необходимо исключить из рассмотрения
|
|
3. Форму и тесноту корреляционной зависимости можно с помощью множественного коэффициента корреляции 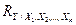 . В частности, если число факторных признаков равно двум, то
. В частности, если число факторных признаков равно двум, то
 .
.
Проверкой правильности произведенных расчетов является требование:
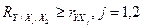 .
.
Если  , то связь между признаками линейная. Если же
, то связь между признаками линейная. Если же  , то связь является линейной и тесной.
, то связь является линейной и тесной.
4. Проверка статистическое значимости эмпирических данных, а следовательно принципиальная возможность построения регрессионной модели, производится с помощью F – критерия Фишера.
Правило проверки гипотезы. Если наблюдаемое значение критерия больше критического,
 ,
,
то это с доверительной вероятностью γ (уровнем значимости α =1- γ) говорит о статистической значимости эмпирических данных. При этом наблюдаемое значение критерия равно
 ,
,
а критическое значение критерия определяется по таблице в зависимости от уровня значимости α =1- γ и числа степеней свободы  и
и  (см. таблицу 4 Приложения),
(см. таблицу 4 Приложения),
 .
.
5. Общий индекс детерминации позволяет определить суммарное влияние факторных признаков на результативный. Он равен:
 .
.
6. После того, как установлена форма корреляционной зависимости, подтверждена гипотеза о статистической значимости эмпирических данных, приступают к построению многофакторной модели регрессии. Например, если модель – линейная, число факторных признаков равно двум, то ее уравнение имеет вид:
 .
.
Параметры модели находятся методом наименьших квадратов путем решения системы нормальных уравнений. Например, в линейном случае для k=2, система имеет вид:
 .
.
Существует другой, упрощенный способ нахождения параметров 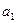 ,
,  и
и  :
:
 ,
,
 ,
,
 .
.
7. Оценка точности регрессионной модели производится также, как и в случае парной регрессии – с помощью средней ошибки аппроксимации 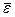 (см. задачу 9, п. 7).
(см. задачу 9, п. 7).
8. С помощью дельта – коэффициента  можно ответить на вопрос: в какой мере факторный признак
можно ответить на вопрос: в какой мере факторный признак  влияет на результативный. Он рассчитывается по формуле:
влияет на результативный. Он рассчитывается по формуле:
 .
.
Проверить правильность произведенных расчетов позволяет следующее равенство:
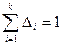 .
.
9. Величина среднего коэффициента эластичности  отвечает на вопрос: на сколько процентов изменится результативный признак, если данный факторный признак
отвечает на вопрос: на сколько процентов изменится результативный признак, если данный факторный признак  изменить на 1%? Он равен:
изменить на 1%? Он равен:
 .
.
10. С помощью значений дельта – коэффициента и среднего коэффициента эластичности можно исключить из модели самый незначимый признак. Им признается тот, у которого одновременно
 ,
,  .
.
Решаем задачу. Вначале, запишем эмпирические данные (объем выборки n =10) в виде таблицы:
| Y | 
| 
| 
| |
Все необходимые расчеты осуществлены в таблице 12. Под таблицей рассчитаем средние значения, дисперсии (по формуле разностей) и средние квадратические отклонения каждого из признаков.
Таблица 12
| у | 
| 
| 
| 
| 
| 
| 
| 
| 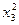
| 
| 
| 
| 
| |

|
Y:  ,
,  ,
,
 ,
,  .
.
 :
:  ,
,  ,
,
 ,
,  .
.
 :
:  ,
,  ,
,
 ,
,  .
.
 :
:  ,
,  ,
,
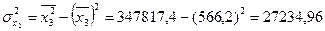 ,
,  .
.
Теперь найдем средние значения произведений признаков:
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 .
.
Вычисляем межфакторные и парные коэффициенты линейной корреляции:
 ,
,
 ;
;
 ,
,
 ;
;
 ,
,
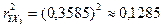 ;
;
 ,
,
 ;
;
 ,
,
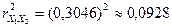 ;
;
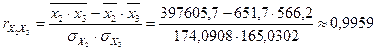 ,
,
 .
.
Займемся отбором факторных признаков в модель.
Сначала с вероятностью 0,95 оценим статистическую значимость каждого из имеющихся факторных признаков. Согласно таблице 3 приложения критическое значение критерия Стьюдента для уровня значимости
α = 1 - 0,95 = 0,05 и числа степеней свободы ν =10 – 2 = 8 равно
 .
.
Вычислим наблюдаемые значения:
 :
:  ;
;
 :
:  ;
;
 :
: 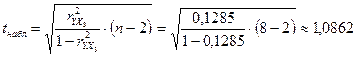 .
.
Видим, что только для признака  выполняется правило проверки гипотезы. Следовательно, он однозначно включается в модель.
выполняется правило проверки гипотезы. Следовательно, он однозначно включается в модель.
Между признаками  и
и  нарушается принцип отсутствия автокорреляции,
нарушается принцип отсутствия автокорреляции,  , связь между ними тесная. Поэтому, один из этих признаков подлежит исключению. Поскольку
, связь между ними тесная. Поэтому, один из этих признаков подлежит исключению. Поскольку  >
>  , то признак
, то признак  исключается из рассмотрения, а признак
исключается из рассмотрения, а признак  - остается.
- остается.
Множественный коэффициент корреляции равен:
 Найденное значение указывает на высокую степень тесноты и линейности корреляционной зависимости.
Найденное значение указывает на высокую степень тесноты и линейности корреляционной зависимости.
С вероятностью 0,95 выдвинем гипотезу о статистической значимости эмпирических данных. Поскольку n = 10, k =2, то α =1-0,95 = 0,05  ,
,  . Согласно таблице 4
. Согласно таблице 4
 .
.
Наблюдаемое значение равно:
 .
.
Правило проверки гипотезы выполнено. Поэтому с вероятностью 0,95 гипотеза о статистической значимости эмпирических данных принимается, корреляционная модель может быть построена.
Общий индекс детерминации равен
 .
.
Следовательно, факторные признаки, отобранные в модель, влияют на
результативный в пределах 59,43%. Это не очень сильное влияние. Согласно закону Парето степень влияния должна быть не меньше 80%.
Линейная модель, описывающая корреляционную зависимость, имеет следующий общий вид:
 .
.
Используя таблицу 12, получаем систему нормальных уравнений:
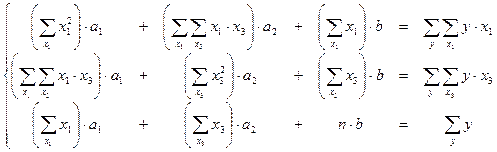 ;
;
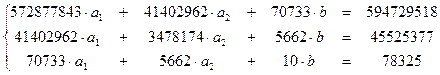 .
.
Решая систему, получаем:
 ,
, 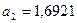 ,
,  .
.
Итак, искомое уравнение регрессии имеет вид:
 .
.
Найдем параметры уравнения регрессии упрощенным способом:

 ,
,
 .
.
Найдем среднюю ошибку аппроксимации. Для этого, подставив значения факторных признаков, соответствующих данному значению y в модель, получаем теоретические значения y*. Вычисления производим в таблице:
| у | 
| 
| 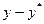
| 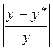
|
| 6672,0838 | 0,3347 | |||
| 7708,8693 | 0,1126 | |||
| 7824,4743 | 0,1337 | |||
| 8461,0588 | 0,1620 | |||
| 6644,8366 | 0,1793 | |||
| 12009,5096 | 0,0804 | |||
| 6574,3001 | 0,3472 | |||
| 6894,8649 | 0,0626 | |||
| 8339,5446 | 0,1715 | |||
| 8642,1934 | 0,0962 | |||

| - | - | - | 1,6801 |
Итак, значение средней ошибки аппроксимации равно
 ,
,
что говорит о низкой точности модели.
Определим значения дельта – коэффициентов. Имеем:
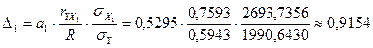 или 91,54%,
или 91,54%,
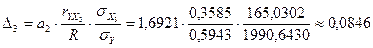 или 8,46%.
или 8,46%.
Сумма дельта – коэффициентов равна 1, следовательно, есть все основания полагать, что вычисления произведены верно. Итак, признак  влияет на признак Y в пределах 91,54%, а степень влияния признака
влияет на признак Y в пределах 91,54%, а степень влияния признака  равна 8,46%.
равна 8,46%.
Найдем величины средних коэффициентов эластичности:
 или 47,82%,
или 47,82%,
 или 12,23%.
или 12,23%.
Таким образом, изменение признака  на 1% влечет за собой изменение признака Y на 47,82%, а вследствие изменения признака
на 1% влечет за собой изменение признака Y на 47,82%, а вследствие изменения признака  , изменение признака Y составит 12,23%
, изменение признака Y составит 12,23%
Перейдем к модели с парной регрессией. Поскольку одновременно минимум дельта – коэффициента и среднего коэффициента эластичности соответствует признаку  ,
,
 ,
,
 ,
,
то он исключается из модели. Итак, общий вид уравнения парной регрессии следующий:
 .
.
Так как 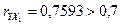 , то согласно выводам задачи 9 связь признается линейной и тесной. Уравнение прямой линии регрессии найдем упрощенным способом (смотри п. 6 задачи 9):
, то согласно выводам задачи 9 связь признается линейной и тесной. Уравнение прямой линии регрессии найдем упрощенным способом (смотри п. 6 задачи 9):  ;
;
 ;
;
 ;
;
 .
.

Для заметок
Тема 4. «Ряды динамики»
Задача 11. Реализацияпродукции магазином (тыс. руб.) в 2006 – 2008 годах характеризовалось следующими данными (на конец месяца):
| Месяц | Реализацияпродукции (на конец месяца, тыс. руб.) | ||
| Январь | 401,3 | 412,5 | 374,6 |
| Февраль | 286,6 | 335,1 | 245,5 |
| Март | 332,5 | 348,5 | 304,6 |
| Апрель | 197,8 | 198,4 | 171,1 |
| Май | 209,7 | 220,8 | 210,8 |
| Июнь | 294,4 | 323,0 | 321,3 |
| Июль | 275,0 | 281,4 | 244,7 |
| Август | 329,7 | 399,0 | 345,6 |
| Сентябрь | 476,5 | 531,8 | 495,4 |
| Октябрь | 503,6 | 551,0 | 523,2 |
| Ноябрь | 408,7 | 428,1 | 385,3 |
| Декабрь | 341,8 | 283,0 | 274,2 |
По данным 2008 года необходимо:
а) определить тип ряда динамики;
б) произвести анализ уровней ряда динамики цепным и базисным способами (за базисный принять уровень января 2008 года);
в) найти средние значения уровней ряда динамики и его числовых характеристик.
1. Рядом динамики называется способ записи случайной величины (признака, фактора) Y, при котором ее значения (уровни)  приведены в зависимости от времени
приведены в зависимости от времени  . Если
. Если  - интервал времени (например, месяц, квартал, год и т. д.), то ряд динамики есть интервальный. Если же значения уровней приведены на определенную дату (например, начало месяца, конец квартала, начало года и т. д.), то ряд динамики есть моментный. Различают также ряды динамики с равноотстоящими и неравноотстоящими по времени уровнями. Ряд динамики принято представлять в виде таблицы:
- интервал времени (например, месяц, квартал, год и т. д.), то ряд динамики есть интервальный. Если же значения уровней приведены на определенную дату (например, начало месяца, конец квартала, начало года и т. д.), то ряд динамики есть моментный. Различают также ряды динамики с равноотстоящими и неравноотстоящими по времени уровнями. Ряд динамики принято представлять в виде таблицы:

| 
| 
| … | 
|

| 
| 
| … | 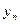
|
2. Сравнение уровней ряда динамики производится двумя способами: цепным и базисным. При первом способе данный уровень 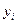 сравнивается с предыдущем ему уровнем
сравнивается с предыдущем ему уровнем  . Во втором случае выбирается базисный уровень
. Во втором случае выбирается базисный уровень  (не обязательно первый) и все остальные уровни сравниваются с ним. Имеют место следующие
(не обязательно первый) и все остальные уровни сравниваются с ним. Имеют место следующие
основные показатели, характеризующие изменения уровней ряда динамики: абсолютный прирост, коэффициент роста, темп роста, темп прироста, абсолютное значение одного процента прироста (расчет этого показателя имеет экономический смысл только на цепной основе). Их расчетные формулы приведены в таблице:
| Показатель | Обозначение | Расчетная формула | |
| Цепной способ сравнения | Базисный способ сравнения | ||
| Абсолютный прирост | 
| 
| 
|
| Коэффициент роста | 
| 
| 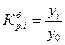
|
| Темп роста | 
| 
| |
| Темп прироста | 
| 
| 
|

| |||
| Абсолютное значение одного процента прироста | |%| |  или
или

| - |
3. В зависимости от типа ряда динамики среднее значение его уровней подсчитывается по формуле:

- если ряд динамики интервальный с равностоящими уровнями;
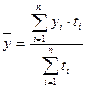
- если ряд динамики интервальный с неравноотстоящими уровнями,
 - временная разность между данным и следующим уровнем,
- временная разность между данным и следующим уровнем,  ;
;
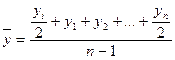
- если ряд динамики моментный с равноотстоящими уровнями;
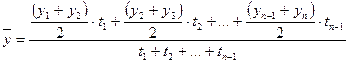
- если ряд динамики моментный с неравноотстоящими уровнями,
 - временная разность между данным и следующим уровнем.
- временная разность между данным и следующим уровнем.
Среднее значение абсолютного прироста равно:
 .
.
Величина среднего значения коэффициента роста равна:
 .
.
Среднее значение темпов роста подсчитывается по формуле:
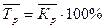 .
.
Наконец, среднее значение темпов прироста рассчитывается следующим образом:
 .
.
Переходим к решению задачи. Так как значения уровней приведены на определенную дату (конец месяца), временная разность между уровнями постоянная (1 месяц), то рассматриваемый ряд динамики является моментным с равноотстоящими уровнями.
Найдем числовые характеристики уровня ряда динамики. Результаты расчетов помещены в таблицу 13.
В качестве примера произведем анализ строки таблицы 13, соответствующей октябрю месяцу. В октябре 2008 года магазин реализовал продукции на 523,2 тыс. руб., что на 27,8 тыс. руб. больше по сравнению с сентябрем и на 148,6 тыс. руб. больше по сравнению с январем 2008 года. Следовательно, реализация продукции в октябре увеличилась в 1,0561 раза по сравнению с октябрем и в 1,3967 раза по сравнению с январем. Уровень реализации в октябре составил 105,6116% от сентябрьского и 139,669% от январского уровня реализации. Таким образом, продукции в октябре реализовано на 5,6116% больше по сравнению с сентябрем и на 39,669% больше по сравнению с январем месяцем. Величина абсолютной величины одного процента прироста составила 4,954 тыс. руб.
Таблица 13

| 
|  , тыс. руб. , тыс. руб.
| 
|  , % , %
|  , % , %
| |%|, тыс. руб. | ||||
| С пред. месяцем | С январем 2008 г. | С пред. месяцем | С январем 2008 г. | С пред. месяцем | С январем 2008 г. | С пред. месяцем | С январем 2008 г. | |||
| 374,6 | - | - | - | - | - | |||||
| 245,5 | -129,1 | -129,1 | 0,6554 | 0,6554 | 65,5366 | 65,5366 | -34,4634 | -34,4634 | 3,746 | |
| 304,6 | 59,1 | -70 | 1,2407 | 0,8131 | 124,0733 | 81,3134 | 24,0733 | -18,6866 | 2,455 | |
| 171,1 | -133,5 | -203,5 | 0,5617 | 0,4568 | 56,1720 | 45,6754 | -43,8280 | -54,3246 | 3,046 | |
| 210,8 | 39,7 | -163,8 | 1,2320 | 0,5627 | 123,2028 | 56,2734 | 23,2028 | -43,7266 | 1,711 | |
| 321,3 | 110,5 | -53,3 | 1,5242 | 0,8577 | 152,4194 | 85,7715 | 52,4194 | -14,2285 | 2,108 | |
| 244,7 | -76,6 | -129,9 | 0,7616 | 0,6532 | 76,1594 | 65,3230 | -23,8406 | -34,6770 | 3,213 | |
| 345,6 | 100,9 | -29 | 1,4123 | 0,9226 | 141,2342 | 92,2584 | 41,2342 | -7,7416 | 2,447 | |
| 495,4 | 149,8 | 120,8 | 1,4334 | 1,3225 | 143,3449 | 132,2477 | 43,3449 | 32,2477 | 3,456 | |
| 523,2 | 27,8 | 148,6 | 1,0561 | 1,3967 | 105,6116 | 139,6690 | 5,6116 | 39,6690 | 4,954 | |
| 385,3 | -137,9 | 10,7 | 0,7364 | 1,0286 | 73,6430 | 102,8564 | -26,3570 | 2,8564 | 5,232 | |
| 274,2 | -111,1 | -100,4 | 0,7117 | 0,7320 | 71,1653 | 73,1981 | -28,8347 | -26,8019 | 3,853 |
Найдем среднее значение уровней ряда динамики. Имеем: среднемесячный объем реализации продукции магазином составил в 2008 году

324,7 (тыс. руб.).
Так как
 ,
,
то заключаем, что ежемесячное падение объемов реализации продукции в 2008 году составляло в среднем 9,1 тыс. руб.
Среднее значение коэффициента роста равно
 .
.
Это означает, что месячный уровень объема реализации составляет в среднем 0,972 от предыдущего месяца или (согласно формуле среднего значения темпов роста)
 .
.
Итак, в среднем в месяц, объем продаж сокращался на 2,8% по сравнению с предыдущим месяцем, так как
 .
.
Задача 12. По данным задачи 11 (рассмотреть данные 2008 года) построить уравнение линейной функции тренда.
На формирование значение уровней ряда динамики основное влияние оказывают долговременные факторы, формирующие общую, в длительной перспективе тенденцию развития признака. Результат действия этих факторов моделируется в виде функции тренда
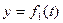 .
.
В частности, если тренд – линейный, то
 .
.
Параметры a и b могут быть найдены методом наименьших квадратов путем решения системы нормальных уравнений:
 .
.
Решая ее, получаем:
 .
.
Все необходимые расчеты делаем в таблице:

| 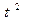
| 
| 
| |
| 374,6 | 374,6 | |||
| 245,5 | ||||
| 304,6 | 913,8 | |||
| 171,1 | 684,4 | |||
| 210,8 | ||||
| 321,3 | 1927,8 | |||
| 244,7 | 1712,9 | |||
| 345,6 | 2764,8 | |||
| 495,4 | 4458,6 | |||
| 523,2 | ||||
| 385,3 | 4238,3 | |||
| 274,2 | 3290,4 | |||

| 3896,3 | 27142,6 |
Получаем:
 ,
,  .
.
Итак, уравнение функции тренда имеет вид:
 .
.
Задача 13. Построить индексы сезонности за 2008 год и за 2006 – 2008 г.г. Результаты представить графически.
Помимо долговременных, на формирование значений уровней ряда динамики оказывают влияния сезонные факторы, определяющие периодическое изменение значений признака в определенные моменты времени (сезоны), причем эти изменения для каждого сезона можно считать постоянной величиной.
Самым простым способом учета сезонных факторов является расчет индексов сезонности, которые для одного года равны:
 ,
,
при этом  - значение уровня ряда динамики в момент времени в данный момент времени (сезон)
- значение уровня ряда динамики в момент времени в данный момент времени (сезон)  , а
, а 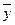 - среднее значение уровней ряда динамики.
- среднее значение уровней ряда динамики.
С целью избежания влияния случайных факторов, на практике, расчет индексов сезонности производится не за один, а за  лет. В этом случае
лет. В этом случае
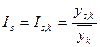 ,
,
Где

- среднее значение уровней ряда динамики,
Date: 2016-05-25; view: 706; Нарушение авторских прав