Белгілер өзгеруі туралы түсінік

Статистикалық өзгерме дегеніміз жиынтық бірліктерінің белгілеріне әртүрлі себептердің әсерінен болған сандық өзгеріс. Өзгерме көрсеткіштерінің жай және салмақталған түрлері болады. Егер сандық қатардың орташа мәні арифметикалық орташа шаманың жай түрімен есептелсе, онда өзгерменің жай түрі қолданылады. Ал жиіліктері бірге беріліп, әр түрлі сандық мәндермен көрсетілетін болса салмақталған түрі қолданылады.

Әлеуметтік-экономикалық құбылыстар ешуақытта тұрақты болмайды, олар үнемі өзгеріп отырады. Олардың жалпы жиынтықтары әр түрлі сандық көрсеткіштермен сипатталады. Осы көрсеткіштердің ауытқуын анықтауда өзгерменің келесідей негізгі көрсеткіштері есептеледі:

-өзгерменің өрісі;

-орташа сызықтық ауытқу;

-шашырандылық;

-орташа шаршылық ауытқу;

-өзгерменің коэффициенті.

Өзгерменің өрісі дегеніміз сандық қатар белгілерінің ең үлкен және ең кіші шамаларының арасындағы айырмашылық. Ол статистикада R-әрпімен белгіленеді және келесі формуламен есептеледі:

R=Xmax- Xmin, мұндағы,

Xmax- сандық қатардың ең үлкен мәні;

Xmin- сандық қатар белгілерінің ең кіші мәні.

Орташа сызықтық ауытқу дегеніміз әрбір белгінің жеке мәнінен арифметикалық орташа шаманы алып, одан шыққан ауытқу қосындыны белгі санына немесе әр қатардағы ауытқу көрсеткіштерін жиіліктеріне көбейтіп, ал оның қосындысын сол жиіліктің жалпы жиынтығына бөлгеннен шыққан шаманы айтады.

Статистикада орташа сызықтық ауытқу d- әрпімен белгіленеді және оны келесі формуламен анықтаймыз:

-жай түрі,

- салмақталған түрі, мұндағы,

Х- белгілердің жеке сандық мәндері;

__

Х- белгілердің орташа шамасы;

n- белгілердің саны;

f- жиілік көрсеткіштерінің жеке мәндері;

- жинақтау (қосынды) белгісі.

Шашыранды (дисперсия) деп әрбір қатардағы белгінің жеке мәнінен арифметикалық орташа шаманы алдындағы айырмаларды екі есе дәрежелеп және бір-біріне қосып, одан шыққан ауытқу қосындыны белгі санына немесе дәрежеленген ауытқу көрсеткіштері жиіліктеріне көбейтіп, оның қосындысын сол жиіліктің жалпы жиынтығына бөлінгеннен шыққан бөліндіні айтады.

Статистикада қорытындылаушы көрсеткіштермен қатар өзгермелі белгілердің бөлінуін қосымша сипаттайтын құрылымдық орта шамалар да қолданылады. Оған мода мен медиана жатады.

Мода дегеніміз статистикалық қатарлардың ішінде ең жиі кездесетін белгінің үлкен шамасы, яғни өзгермелі сандық қатарда жиіліктің үлкен мәні жатқан белгі.

Егер статистикалық қатардың белгісі бүтін санмен берілсе, сол берілген белгінің ең үлкен жиілік мәні жатқан қатар мода болып саналады.

Егер статистикалық қатарлар белгілерінің ең үлкен жиілік мәні бірдей екі сандық көрсеткішпен берілсе, онда модалық белгі екеу болады. Ал жиілік мәндері бірдей бірнеше белгі берілетін болса, онда модалық көрсеткіш болмайды.

Қатар белгілері деңгей аралықты шамамен берілсе, онда еңбірінші ең үлкен жиілігі бар қатар анықталады, одан кейін модалық белгінің деңгей аралығының айырмасы есептеледі, ол модалық қатардың үлкен мәнінен кіші мәнін алғанға тең болады.

Статистикада мода Мо -әрпімен белгіленеді және деңгей аралықты қатар берілген болса, келесі формуламен анықталады:

F Mo –fMo-1

Mo=XMo+dMo ----------------------------------------------,мұндағы,

(f Mo –fMo-1)+(f Mo –fMo+1)

XMo- модалық қатардың деңгей аралығының кіші мәні;

dMo –модалық қатардың деңгей аралығының айырмасы;

f Mo –модалық қатардың жиілігі;

fMo-1—модалық қатардың алдыңғы қатар жиілігі;

fMo+1- модалық қатардан кейінгі қатар жиілігі.

Медиана дегеніміз статистикалық қатардың ортасында жатқан белгі. Ол қатарды тең етіп екіге бөледі және оның екі жағындағы белгілердің сандық бірліктері бірдей болады.

Медиана статистикада Ме- әрпімен белгіленеді. Егер қатардың белгісі бүтін санмен берілсе, медиананы анықтау үшін белгінің рет санына бірді қосып, шыққан қосындыны екіге бөлеміз, ол келесі формуламен анықталады:

, мұндағы, n-қатар саны

Егер қатар белгісі бүтін санмен және жиілікпен берілсе, медиананы есептеу үшін жиіліктің жинақталған қосындысын тең екіге бөліп, шыққан көрсеткішке ½-ді қосамыз.

F Me 1

Me= ------------ + -----.

2 2

Егер қатар белгісі деңгей аралықты шамамен берілсе, онда алдымен медианалық қатарды анықтаймыз. Ол үшін әрбір жиілікке келесісін қоса отырып, жинақталған жиілік қосындысын есептейміз.

Деңгей аралықты қатардан медиананы есептеу үшін келесі формула қолданылады:

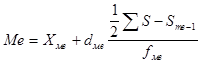, мұндағы,

XMе- медианалық қатардың деңгей аралығының кіші мәні;

dMе –медианалық қатардың деңгей аралығының айырмасы;

S –медианалық қатардың қосындысы;

S Mе-1—медианалық қатардың алдыңғы қатардағы жинақталған жиілік қосындысы.

Date: 2016-05-25; view: 1261; Нарушение авторских прав