
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Критерии выбора стратегий при игре с природой
|
|
Все критерии продемонстрируем на игре с природой, соответствующей первому варианту постановки, как более общему.
Применение критериев рассмотрим на следующем примере. Фирма Исполнитель выполняет и сдает проект. На этапе выполнения возможны следующие стратегии: C 1 – выполнение собственными силами; C 2 – привлече-
ние только научных консультантов; C 3 – привлечение только финансовых консультантов; C 4 – привлечение научных и финансовых консультантов. Ре-
зультат сдачи проекта зависит от требовательности Заказчика, который может: П 1 – не проводить экспертиз; П 2 – провести только научную эксперти-
зу; П 3 – провести научную и экономическую экспертизу; экономическая экспертиза без научной не проводится. Чем больше проверок проекта, тем меньший финансовый результат можно ожидать, особенно, если не были привлечены соответствующие эксперты(из-заустранения несоответствий, переносов сроков сдачи и т.п.). Однако и привлечение консультантов влечет дополнительные затраты. Известно, что Заказчик имеет некоторую степень доверия к консультантам и при их привлечении вероятность соответствующей проверки снижается. Заметим, что Заказчик в этой ситуации не имеет заинтересованности в финансовом результате работы Исполнителя и может рассматриваться как Природа. Несмотря на свою осознанность, он имеет свои собственные интересы – качественный результат выполнения заказа, сроки выполнения и т.п. Эти интересы слабо коррелируют с доходом Исполнителя, т.к. общая стоимость работ обычно оговаривается заранее.
Пусть финансовый результат для Исполнителя (в млн. руб.) и вероятности проверок Заказчика могут быть оценены заранее и сведены в таблицу игры с природой Таб. 4.
Таблица 4.
Игра с природой для примера Исполнитель – Заказчик
| П 1 | П 2 | П 3 | ||||
| C 1 | 0,3 | 0,3 | 0,4 | |||
| C 2 | 0,6 | 0,1 | 0,3 | |||
| C 3 | 0,5 | 0,4 | 0,1 | |||
| C 4 | 0,8 | 0,1 | 0,1 |
Рассмотрим несколько значений в ячейках таблицы.
Значения 10 и 0,3 в ячейке C 1 П 1 показывают, что если Исполнитель выполнит проект самостоятельно, а Заказчик не будет организовывать проверок, то Исполнитель получит 10 млн. руб. Вероятность того, что Заказчик не будет организовывать проверку, если Исполнитель выполнил работу самостоятельно, равна 0,3 или 30%.
Если же в этом случае Заказчик организует обе проверки (ячейка C 1 П 3), то финансовый результатфирмы-исполнителяпадает до 2 млн. руб.
из-занеобходимости значительной доработки проекта. Вероятность такого события при самостоятельном выполнении работ равна 0,4 или 40%.

Значения 5 и 0,1 в ячейке C 4 П 3 показывают, что если Исполнитель привлечет к проекту научных и финансовых консультантов, то при организации обеих проверок Исполнитель получит уже 5 млн. руб., так как проект будет выполнен с учетом многих требований. Вероятность того, что Заказчик будет организовывать обе проверки в этом случае равна 0,1 или 10%. Если же в этом случае Заказчик не будет организовывать экспертной проверки вовсе (вероятность чего очень велика и равна 0,8 или 80%), то выигрыш фир-мы-исполнителясоставит только 6 млн. руб., а не 10, так как велики будут расходы на привлечение консультантов.
БИМАТРИЧНЫЕ ИГРЫ
Впредыдущих главах мы исследовали антагонистические игры. Теперь рассмотрим общий случай игр двух игроков на конечных множествах стратегий с интересами, не являющимися противоположными (то есть неантагонистическими): у каждого игрока имеется своя функция выигрыша, не обязательно противоположная функции выигрыша противника.
Определение. Биматричной игрой называется система из четырех элементов Г= (Х, Y, F, G), где X ={1,…, n }, Y ={1,…, m }- конечные множества стратегий игроков 1 и 2 соответственно; F (i,j) и G (i,j) - их функции выигрыша.
Функции выигрыша F и G можно задать матрицами А =(aij) и B =(bij) (i =1,…, n; j =1,…, m). Смешанные стратегии игроков и функции выигрыша для таких стратегий определяются так же, как и в матричных играх. Далее под биматричной игрой понимается игра со смешанными стратегиями.
Определение. Пара стратегий (x 0, y 0) называется ситуацией
| равновесия биматричной игры, если справедливы соотношения | ||||||||||||||||||||
| F( | (6.1) | |||||||||||||||||||
| x | x, y 0 ) ≤ F(x 0, y 0 ); | |||||||||||||||||||
| G( | , | ) ≤ G( | , | ). | (6.2) | |||||||||||||||
| y | x 0 | y | x 0 | y 0 |
Смысл ситуации равновесия состоит в том, что каждому игроку невыгодно односторонне отступать от входящей в ситуацию стратегии. Таким образом, понятие ситуации равновесия обобщает понятие седловой точки матричной игры.
Представляет определенный интерес оптимальность в смысле, отличном от того, который дает понятие ситуации равновесия.
Определение. Пара стратегий(x 0, y 0)называется оптимальной по Парето, если не существует другой пары стратегий(x, y), такой, что
F (x, y 0)≥ F (x 0, y 0), G (x 0, y)≥ G (x 0, y 0)
(притом хотя бы одно из неравенств является строгим).
Содержательно оптимальность по Парето означает следующее: нет другой ситуации, которая была бы строго предпочтительнее для обоих игроков.
Формальное различие между ситуацией равновесия и ситуацией, оптимальной по Парето, следующее: в первой ни один игрок, действуя в одиночку, не может увеличить своего собственного выигрыша, а во второй оба игрока, действуя совместно, не могут (даже нестрого) увеличить выигрыш каждого. Выбор Парето-оптимальнойпары стратегий может приводить к ситуациям, более выгодным для обоих участников, чем ситуации равновесия.
22. КОРПОРАТИВНЫЕ ИГРЫ.
В России при построении математической модели конфликта делают различия между коалицией действия и коалицией интересов. Коалицией действия называются те или иные коллективы, участвующие в игре и принимающие решения. Коалицией интересов называются коллективы, участвующие в игре и отстаивающие некоторые общие интересы. Кроме того, вводится понятие ситуации - результат выбора всеми коалициями действия своих стратегий.
Игра называется кооперативной, или коалиционной, если игроки могут объединяться в группы, беря на себя некоторые обязательства перед другими игроками и координируя свои действия. Этим она отличается от некооперативных игр, в которых каждый обязан играть за себя. Развлекательные игры редко являются кооперативными, однако такие механизмы нередки в повседневной жизни.
Часто предполагают, что кооперативные игры отличаются именно возможностью общения игроков друг с другом. В общем случае это неверно. Существуют игры, где коммуникация разрешена, но игроки преследуют личные цели, и наоборот.
Из двух типов игр, некооперативные описывают ситуации в мельчайших деталях и выдают более точные результаты. Кооперативные рассматривают процесс игры в целом. Попытки объединить два подхода дали немалые результаты. Так называемая программа Нэша уже нашла решения некоторых кооперативных игр как ситуации равновесия некооперативных игр.
Гибридные игры включают в себя элементы кооперативных и некооперативных игр. Например, игроки могут образовывать группы, но игра будет вестись в некооперативном стиле. Это значит, что каждый игрок будет преследовать интересы своей группы, вместе с тем стараясь достичь личной выгоды.
Кооперативные игры получаются в тех случаях, когда, в игре n игроков разрешается образовывать определённые коалиции. Обозначим через N множество всех игроков, N ={1, 2,..., n}, а через K - любое его подмножество. Пусть игроки из K договариваются между собой о совместных действиях и, таким образом, образуют одну коалицию. Очевидно, что число таких коалиций, состоящих из r игроков, равно числу сочетаний из n по r, то есть 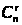 , а число всевозможных коалиций равно
, а число всевозможных коалиций равно
 = 2n - 1.
= 2n - 1.
Из этой формулы видно, что число всевозможных коалиций значительно растёт в зависимости от числа всех игроков в данной игре. Для исследования этих игр необходимо учитывать все возможные коалиции, и поэтому трудности исследований возрастают с ростом n. Образовав коалицию, множество игроков K действует как один игрок против остальных игроков, и выигрыш этой коалиции зависит от применяемых стратегий каждым из n игроков.
Функция u, ставящая в соответствие каждой коалиции K наибольший, уверенно получаемый его выигрыш u (K), называется характеристической функцией игры. Так, например, для бескоалиционной игры n игроков u (K) может получиться, когда игроки из множества K оптимально действуют как один игрок против остальных NK игроков, образующих другую коалицию (второй игрок).
Характеристическая функция u называется простой, если она принимает только два значения: 0 и 1. Если характеристическая функция u простая, то коалиции K, для которых u (K) =1, называются выигрывающими, а коалиции K, для которых u (K) = 0, - проигрывающими.
Если в простой характеристической функции u выигрывающими являются те и только те коалиции, которые содержат фиксированную непустую коалицию R, то характеристическая функция u, обозначаемая в этом случае через uR, называется простейшей.
Содержательно простые характеристические функции возникают, например, в условиях голосования, когда коалиция является выигрывающей, если она собирает более половины голосов (простое большинство) или не менее двух третей голосов (квалифицированное большинство).
Более сложным является пример оценки результатов голосования в Совете безопасности ООН, где выигрывающими коалициями являются все коалиции, состоящие из всех пяти постоянных членов Совета плюс ещё хотя бы один непостоянный член, и только они.
Простейшая характеристическая функция появляется, когда в голосующем коллективе имеется некоторое “ядро", голосующее с соблюдением правила “вето", а голоса остальных участников оказываются несущественными.
Обозначим через uG характеристическую функцию бескоалиционной игры. Эта функция обладает следующими свойствами:
персональность
uG (Ж) = 0,т.е. коалиция, не содержащая ни одного игрока, ничего не выигрывает;
супераддитивность
uG (KИL) і uG (K) + uG (L), если K, L М N, KЗL № Ж,
т.е. общий выигрыш коалиции не меньше суммарного выигрыша всех участников коалиции;
дополнительность
uG (K) + u (NK) = u (N) 
т.е. для бескоалиционной игры с постоянной суммой сумма выигрышей коалиции и остальных игроков должна равняться общей сумме выигрышей всех игроков.
Распределение выигрышей (делёж) игроков должно удовлетворять следующим естественным условиям: если обозначить через xi выигрыш i-го игрока, то, во-первых, должно удовлетворяться условие индивидуальной рациональности
xi і u (i), для i ОN 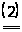
т.е. любой игрок должен получить выигрыш в коалиции не меньше, чем он получил бы, не участвуя в ней (в противном случае он не будет участвовать в коалиции); во-вторых, должно удовлетворяться условие коллективной рациональности
 = u (N)
= u (N) 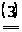
т.е. сумма выигрышей игроков должна соответствовать возможностям (если сумма выигрышей всех игроков меньше, чем u (N), то игрокам незачем вступать в коалицию; если же потребовать, чтобы сумма выигрышей была больше, чем u (N), то это значит, что игроки должны делить между собой сумму большую, чем у них есть).
Таким образом, вектор x = (x1,..., xn), удовлетворяющий условиям индивидуальной и коллективной рациональности, называется дележём в условиях характеристической функции u.
Система {N, u}, состоящая из множества игроков, характеристической функции над этим множеством и множеством дележей, удовлетворяющих соотношениям (2) и (3) в условиях характеристической функции, называется классической кооперативной игрой.
Кооперативная игра с множеством игроков N и характеристической функцией u называется стратегически эквивалентной игрой с тем же множеством игроков и характеристической функцией u1, если найдутся такие к > 0 и произвольные вещественные Ci (iОN), что для любой коалиции К М N имеет место равенство:
u1 (K) = k u (K) + 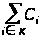

Смысл определения стратегической эквивалентности кооперативных игр (с. э. к. и) состоит в том что характеристические функции с. э. к. и. отличаются только масштабом измерения выигрышей k и начальным капиталом Ci. Стратегическая эквивалентность кооперативных игр с характеристическими функциями u и u1 обозначается так u~u1. Часто вместо стратегической эквивалентности кооперативных игр говорят о стратегической эквивалентности их характеристических функций.
Справедливы следующие свойства для стратегических эквивалентных игр:
1. Рефлексивность, т.е. каждая характеристическая функция эквивалентна себе u~u.
2. Симметрия, т.е. если u~u1, то u1~u.
3. Транзитивность, т.е. если u~u1 и u1~u2, то u~u2.
Date: 2016-05-25; view: 560; Нарушение авторских прав