Основные определения и теоремы теории игр

Теория игр относится к разделу прикладной математики исследующей математические модели принятия решений в условиях конфликта, противоречий и неопределенности. Задачей теории игр является нахождение оптимальной стратегии поведения в условиях конфликта, неопределенности или противодействия какой то стороны в этой ситуации независимо от того сознательно или неосознанно это происходит. Игровые математические модели позволяют не только найти оптимальную стратегию, которая не всегда однозначна, но и оценить каждый вариант решения с различных иногда противоречивых точек зрения, а так же глубже разобраться во всех сложностях и неопределенностях реальной ситуации для принятия до конца продуманного решения.

Началом теории игр как последовательной математической теории поведения можно считать выход в свет 50 лет назад монографии Дж. фон Неймана и О. Моргенштерна. Французский математик Э. Мулен так характеризует значение теории игр для социально-экономических наук: «По нашему мнению, теория игр представляет собой набор инструментов для построения моделей в экономических и политических теориях. Единственным, но вполне достаточным оправданием существования теории игр служит её растущее применение в этих дисциплинах. Она является поистине неиссякаемым источником гибких концепций, каждая из которых проливает свет на определенные стороны социальных взаимоотношений.».

Вначале введем несколько фундаментальных понятия теории игр, после этого дадим определение этому разделу прикладной математики.

Конфликт - это противоречие, вызванное противоположными интересами сторон.

Конфликтная ситуация - ситуация в которой участвуют стороны интересы которых полностью или частично противоположны.

Игра -это действительный или формальный конфликт, в котором имеется по крайней мере два участника, каждый из которых стремится к достижению собственных целей

Правилами игры называют допустимые действия каждого из игроков, направленные на достижение некоторой цели.

Платежом называется количественная оценка результатов игры.

Парная игра - игра в которой участвуют только две стороны (два игрока).

Игра с нулевой суммой - парная игра при которой сумма платежа равна нулю, т. е. если проигрыш одного игрока, равен выигрышу другого.

Стратегия игрока - это однозначный выбор игрока в каждой из возможных ситуаций, когда этот игрок должен сделать личный ход.

Оптимальная стратегия - это такая стратегия игрока, которая при многократном повторении игры обеспечивает ему максимально возможный средний выигрыш или минимально возможный средний проигрыш.

Пусть мы имеем парную игру с нулевой суммой, один игрок может выбрать при данном ходе i-ю стратегию изmсвоих возможных (i=1..m), а второй, не зная выбора первогоj-ю стратегию изnсвоих возможных стратегий (j=1..n). В результате первый игрок выигрывает величину, а второй проигрывает эту величину. Из этих величин составим матрицуA.

A

Платежная матрица - так назовем матрицуAили еще по другому матрицей игры.

Конечной игрой размерности (m ´ n) называется игра определенная матрицей А имеющей m строк и n столбцов.

Максимином или нижней ценой игры назавем число,

а соответствующая ему стратегия (строка) максиминной.

Минимаксом или верхней ценой игры назавем число

,

а соответствующая ему стратегия (столбец) минимаксной.

Теорема 1.1. Нижняя цена игры всегда не превосходит верхнюю цену игры.

Игрой с седловой точкой называется игра для которой.

Ценой игры называется величина, если.

В случае игры с седловой точкой, игрокам выгодно придерживатся максиминной и минимаксной стратегий и не выгодно отклонятся от них. В таких случаях про игру говорят, что в ней имеет место равновесие в чистых стратегиях.

Возможна игра и с несколькими седловыми точками. Тогда игра имеет несколько оптимальных решений, но с одинаковой ценой игры.

Чаще встречаются матричные игры без седловой точки, когда a < b и тогда для нахождения её решения используются смешанные стратегии.

Смешанной стратегией игрока называется вектор, каждая из компонент которого показывает относительную частоту использования игроком соответствующей чистой стратегии.

Теорема 1.2. Основная теорема теории матричных игр. Всякая матричная игра с нулевой суммой имеет решение в смешанных стратегиях.

Теорема 1.3. Если один из игроков применяет оптимальную смешанную стратегию, то его выигрыш равен цене игры n в не зависимости от того, с какими частотами будет применять второй игрок свои стратегии (в том числе и чистые стратегии

16.АНАЛИТИЧЕСКОЕ РЕШЕНИЕ ИГРЫ ТИПА 2X2/ Аналитический метод решения игры типа 2 х 2

Рассмотрим игру без седловой точки типа 2 х 2 с платежной матрицей

и найдем оптимальную стратегию

игрока А. Согласно следствию 3 из основной теоремы теории игр эта стратегия обеспечивает игроку А выигрыш, равный цене игры V, даже если игрок В не выходит за пределы своих полезных стратегий. В данной игре обе чистые стратегии игрока В являются полезными, поскольку в противном случае игра имела бы решение в области чистых стратегий, т.е. была бы игрой с седловой точкой.

Отсюда вытекает, что неизвестные удовлетворяют следующей системе из трех линейных уравнений

решение которой имеет вид

Аналогичным образом можно найти оптимальную стратегию

игрока В. В этом случае неизвестные удовлетворяют системе уравнений

решение которой имеет вид

Применим теперь полученные формулы к карточной игре типа «веришь – не веришь».

Пример 6.1. Имеются две карты: туз и двойка. Игрок А наугад берет одну из них. Если А взял туза, то он заявляет: «У меня туз» и требует от противника рубль. Если же А взял двойку, то он может либо сказать: «У меня туз» и потребовать рубль, либо признаться, что у него двойка и заплатить рубль. Игрок В, если ему предлагают рубль, берет его. Однако, если у него требуют рубль, то В может либо поверить, что у А туз, и заплатить рубль, либо не верить и потребовать проверки. Если в результате проверки окажется, что у А действительно туз, то В платит 2 рубля. Если же выяснится, что у А была двойка, то А платит 2 рубля.

Найти оптимальные стратегии для каждого из игроков.

Решение. У игрока А есть 2 стратегии: А ₁ – обманывать, А ₂ – не обманывать. У игрока В тоже есть 2 стратегии: В ₁ – верить, В ₂ – не верить. Это позволяет найти все элементы платежной матрицы игры, вычислив средний выигрыш для каждой комбинации стратегий.

1. А ₁ В ₁ (А обманывает, В верит).

Если А берет туза (вероятность этого 0,5), то он требует рубль. В верит ему и платит. Если А берет двойку (вероятность этого также 0,5), то он обманывает и тоже требует рубль. В верит ему и платит. Средний выигрыш А равен .

2. Комбинация А ₁ В ₂ (А обманывает, В не верит).

Если А берет туза, то он требует рубль, а В не верит и после проверки платит 2 рубля. Если же А взял двойку, то он обманывает и тоже требует рубль. В не верит ему, и в результате А платит 2 рубля. Средний выигрыш А равен .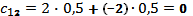

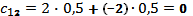3. Комбинация А ₂ В ₁ (А не обманывает, В верит).

Если А берет туза, то он требует рубль, В платит 1 рубль. Если А берет двойку, то он сообщает об этом и платит рубль. Средний выигрыш А равен .

4. Комбинация А ₂ В ₂ (А не обманывает, В не верит).

Если А берет туза, то он требует рубль, В проверяет и платит 2 рубля. Если А берет двойку, то он сообщает об этом и платит рубль. Средний выигрыш А равен .

Отсюда вытекает, что платежная матрица имеет вид

и можно найти нижнюю и верхнюю цены игры:

Следовательно, игра не имеет седловой точки, и ее решение нужно искать в области смешанных стратегий. Для этого воспользуемся формулами полученными выше:

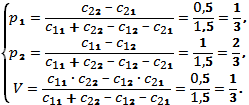
Следовательно, смешанная стратегия игрока А имеет вид

.

Далее получаем

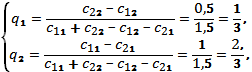
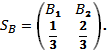
Таким образом, оптимальным для А будет в одной трети случаев обманывать, а в двух третях случаев – не обманывать. Такая тактика обеспечит ему средний выигрыш, равный V =1/3. Если бы А стал пользоваться своей максиминной стратегией, то его выигрыш был бы равен .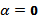

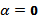Для В оптимальная стратегия – это в одной трети случаев верить А и платить ему рубль, а в остальных случаях требовать проверки. В этой ситуации его средний проигрыш составит 1/3, тогда как при применении минимаксной стратегии он будет проигрывать в среднем

Значение V =1/3 показывает, что рассмотренная игра выгодна для А и невыгодна для В, поскольку, пользуясь своей оптимальной стратегией, А всегда может обеспечить себе положительный средний выигрыш.

17.ГРАФИЧЕСКОЕ РЕШЕНИЕ. Графический метод решения игр типа 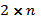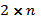и

Рассмотрим игру типа 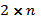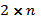с платежной матрицей

и проведем через точку (1;0) координатной плоскости Oxy прямую l, перпендикулярно оси абсцисс. После этого для каждой из стратегий B_i (i=1,2,…,n) проведем прямую

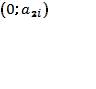
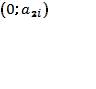соединяющую точку на оси Oy с точкой на прямой l. Ось Oy отвечает за стратегию А ₁, а прямая l – за стратегию А ₂.

Если игрок А применяет смешанную стратегию

то его выигрыш в случае, если противник применяет чистую стратегию В_i, равен

и этому выигрышу соответствует М на прямой b_i с абсциссой x=p₂.

Ломанная b₁MNb ₃, отмеченная на чертеже жирной линией, позволяет определить минимальный выигрыш игрока А при любом поведении игрока В. Точка N, в которой эта ломанная достигает максимума, определяет решение и цену игры. Ордината точки N равна цене игры V, а ее абсцисса p ₂ – частоте применения стратегии A ₁ в оптимальной смешанной стратегии игрока А.

Далее непосредственно по чертежу находим пару «полезных» стратегий игрока В, пересекающихся в точке N (если в точке N пересекается более двух стратегий, то выберем любые две из них). Пусть это будут стратегии B_i и B_j. Поскольку выигрыш игрока А, если он придерживается оптимальной стратегии, не зависит от того, в каких пропорциях игрок В применяет эти стратегии, то неизвестные p ₁, p ₂, V определяются из системы уравнений

Частоты q₁, q₂ в оптимальной стратегии

игрока В определяются из соотношения

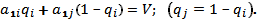
Замечание. Иногда точка N не является пересечением двух стратегий, а попадает на одну из прямых х =0 или х =1. В этом случае решением игры будут соответствующие чистые стратегии.

Для игры решение находится совершенно аналогично. Действительно, поскольку выигрыш игрока А одновременно является проигрышем игрока В, то для решения задачи нужно построить ломанную, соответствующую верхней границе выигрыша игрока А, а затем найти на ней точку с минимальной ординатой.

Пример 7.1. Пусть игра задана матрицей

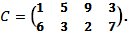
Найти оптимальные стратегии игроков и определить цену игры.

Решение.

Проведем прямые b_i, и построим ломанную линию b₁NMb ₃, соответствующую нижней границе выигрыша. Точка N, в которой эта ломанная достигает максимума, является пересечением прямых

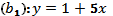
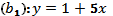и

Вычислив координаты точки N: х ₀=4/7, у ₀=27/7, получаем оптимальную стратегию игрока А

и цену V =27/7. Так как точка N является пересечением прямых b ₁ и b ₂, то полезными стратегиями игрока В будут стратегии B₁ и B₂. Найдем частоты их применения q ₁ и q ₂, зная, что выигрыш равен цене игры, если игрок В применяет оптимальную стратегию, а игрок А – любую из своих полезных стратегий, например стратегию A₁:

=>

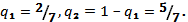
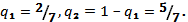
Ответ.

Пример 7.2. Пусть игра задана матрицей

Найти оптимальные стратегии игроков и определить цену игры.

Решение.

Воспользовавшись тем, что игрок В располагает двумя чистыми стратегиями, построим прямые а_i, соответствующие выигрышам игрока А при чистых стратегиях A_i, и ломанную линию a ₁ PNMa ₄, огибающую график сверху. Эта ломанная достигает минимума в точке N (x ₀, y ₀), которая является пересечением прямых

и

Следовательно, х ₀=0,6; V =7,2. и оптимальной стратегией игрока В является стратегия

Цена игры V =7,2. Полезными стратегиями игрока А являются стратегии А ₂ и А ₃. Найдем их частоты р ₂ и р ₃:

Ответ.

18.СМОТРЕТЬ 17.

19. Сведение игры к ЗЛП.

Date: 2016-05-25; view: 1452; Нарушение авторских прав