Игра с нулевой суммой

Теория игр -- это раздел прикладной математики, точнее -- исследования операций. Чаще всего методы теории игр находят применение в экономике, чуть реже в других общественных науках -- социологии, политологии, психологии, этике и других. Начиная с 1970-х годов её взяли на вооружение биологи для исследования поведения животных и теории эволюции. Очень важное значение она имеет для искусственного интеллекта и кибернетики, особенно с проявлением интереса к интеллектуальным агентам2 Представление игр

Игры представляют собой строго определённые математические объекты. Игра образуется игроками, набором стратегий для каждого игрока и указания выигрышей, или платежей, игроков для каждой комбинации стратегий. Большинство кооперативных игр описываются характеристической функцией, в то время как для остальных видов чаще используют нормальную или экстенсивную форму.

Экстенсивная форма

Игра «Ультиматум» в экстенсивной форме

Игры в экстенсивной, или расширенной, форме[4] представляются в виде ориентированного дерева, где каждая вершина соответствует ситуации выбора игроком своей стратегии. Каждому игроку сопоставлен целый уровень вершин. Платежи записываются внизу дерева, под каждой листовой вершиной.

На рисунке слева -- игра для двух игроков. Игрок 1 ходит первым и выбирает стратегию F или U. Игрок 2 анализирует свою позицию и решает -- выбрать стратегию A или R. Скорее всего первый игрок выберет U, а второй -- A (для каждого из них это оптимальные стратегии); тогда они получат соответственно 8 и 2 очка.

Экстенсивная форма очень наглядна, с её помощью особенно удобно представлять игры с более чем двумя игроками и игры с последовательными ходами. Если же участники делают одновременные ходы, то соответствующие вершины либо соединяются пунктиром, либо обводятся сплошной линией

2.что называется матричной игрой.

атричные игры

понятие игр теории (См. Игр теория). М. и. — игры, в которыхучаствуют два игрока (I и II) с противоположными интересами, причём каждый игрок имеет конечное числочистых стратегий (См. Стратегия). Если игрок I имеет m стратегий, а игрок II — n стратегий, то игра может бытьзадана (m × n)-maтрицей А = || a _ij||, где a _ij есть выигрыш игрока I, если он выберет стратегию i (i = -1,..., m), аигрок II — стратегию j (j = 1,..., n). Следуя общим принципам поведения в антагонистических играх (См.Антагонистические игры) (частным случаем которых являются М. и.), игрок I стремится выбрать такуюстратегию i₀, на которой достигается

;

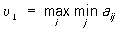
игрок II стремится выбрать стратегию j_o, на которой достигается

;

Если υ₁ = υ₂, то пара(i₀, j₀) составляет седловую точку игры, то есть выполняется двойное неравенство

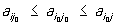
; i = 1, …, m; j = 1, …, n.

Число i₀, j₀ называются оптимальным и чистыми стратегиями игроков I и II соответственно. Если υ₁ ≠υ₂, то всегда υ₁ < υ₂; в этом случае в игре седловой точки нет, а оптимальные стратегии игроков следуетискать среди их смешанных стратегий (то есть вероятностных распределений на множестве чистыхстратегий). В этом случае игроки оперируют уже с математическими ожиданиями выигрышей.

Основная теорема теории М. и. (теорема Неймана о минимаксе) утверждает, что в любой М. и.существуют оптимальные смешанные стратегии х*, у*, на которых достигаемые «минимаксы» равны (общееих значение есть значение игры). Например, игра с матрицей 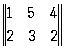i₀ = 2, j₀ = 1, а значение игры равно 2;игра с матрицей х* = (³/₄, ¹/₄), y* = (¹/₂, ¹/₂); значение игры равно ¹/₂.

Для фактического нахождения оптимальных смешанных стратегий чаще всего используют возможностьсведения М. и. к задачам линейного программирования (См. Линейное программирование). Можноиспользовать так называемый итеративный метод Брауна — Робинсон, состоящий в последовательномфиктивном «разыгрывании» данной игры с выбором игроками в каждой данной партии своих чистыхстратегий, наилучших против накопленных к этому моменту стратегий оппонента. Игры, в которых один изигроков имеет только две стратегии, просто решить графически.

М. и. могут служить математическими моделями многих простейших конфликтных ситуаций из областиэкономики, математической статистики, военного дела, биологии. Нередко в качестве одного из игроковрассматривают «природу», под которой понимается вся совокупность внешних обстоятельств, неизвестныхпринимающему решения лицу (другому игроку).

3.что называется матричной игрой типа M xN

Игра с нулевой суммой

Игра с нулевой суммой - особая разновидность игр с постоянной суммой, то есть таких, где игроки не могут увеличить или уменьшить имеющиеся ресурсы, или фонд игры. В этом случае сумма всех выигрышей равна сумме всех проигрышей при любом ходе.

Примерами таких игр может служить покер, где один выигрывает все ставки других; реверси, где захватываются фишки противника; либо банальное воровство.

Многие изучаемые математиками игры, в том числе уже упоминавшаяся “Дилемма заключённого”, иного рода: в играх с ненулевой суммой выигрыш какого-то игрока не обязательно означает проигрыш другого, и наоборот. Исход такой игры может быть меньше или больше нуля. Такие игры могут быть преобразованы к нулевой сумме — это делается введением фиктивного игрока, который “присваивает себе” излишек или восполняет недостаток средств.

Ещё игрой с отличной от нуля суммой является торговля, где каждый участник извлекает выгоду. Сюда также относятся го, шашки и шахматы; в двух последних игрок может превратить свою рядовую фигуру в более сильную, получив преимущество. Во всех этих случаях сумма игры увеличивается. Широко известным примером, где она уменьшается, является война.

Date: 2016-05-25; view: 678; Нарушение авторских прав