Что называется решением игр в смешаной СТ. Решение игры в смешанных стратегиях

Среди конечных игр, имеющих практическое значение, не так уж часто встречаются игры с седловой точкой; более типичным является случай, когда нижняя и верхняя цены игры различны. Анализируя матрицы таких игр, мы пришли к выводу, что если каждому игроку предоставить выбор одной-единственной чистой стратегии, то в расчете на разумного противника этот выбор должен определяться принципом минимакса. При этом игрок А гарантирует себе выигрыш, равный нижней цене игры а. Возникает вопрос: нельзя ли гарантировать выигрыш, больший а, если применять не одну-единственную, «чистую» стратегию, а чередовать случайным образом несколько стратегий? Такие стратегии, состоящие в случайном чередовании чистых стратегий, называются в теории игр смешанными. При пользовании смешанной стратегией перед каждой партией игры пускается в ход какой-то механизм случайного выбора (бросание монеты, игральной кости или вычисление машинойслучайного числа от 0 до 1), обеспечивающий появление каждой стратегии с некоторой вероятностью, и затем принимается та стратегии на которую пал жребий

Смешанные стратегии представляют собой математическую модель изменчивой, гибкой тактики, при которой противник не знает, и не может узнать заранее, с какой обстановкой ему придется встретиться. Таким случайным чередованием приемов (разумеется, без четко определенных вероятностей) часто пользуются в карточных играх.

Введем специальное обозначение для смешанных стратегий. Пусть имеется игра И, в которой у нас стратегий: , а у противника стратегий: Будем обозначать

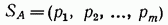
нашу смешанную стратегию, в которой стратегии 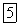применяются с вероятностями причем

Аналогичное обозначение для смешанной стратегии противника будет

где

Очевидно, каждая чистая стратегия является частным случаем смешанной все стратегии, кроме данной, имеют вероятности, равные нулю, а данная — единице.

Оказывается, если допустить не только чистые, но и смешанные стратегии, то можно для каждой конечной игры найти решение, т. е. пару устойчивых оптимальных стратегий игроков.

Решением игры называется пара оптимальных стратегий , в общем случае смешанных, обладающих следующим свойством: если один из игроков придерживается своей оптимальной стратегии, то другому не может быть выгодно отступать от своей.

Выигрыш, соответствующий решению, называется ценой игры; мы будем (как раньше — чистую цену) обозначать ее

Существует так называемая основная теорема теории игр, состоящая в следующем.

Каждая конечная игра имеет по крайней мере одно решение, возможно, в области смешанных стратегий.

Мы не будем останавливаться на строгом доказательстве этой теоремы, тем более, что в дальнейшем существование решения игры будет достаточно очевидно из других соображений.

Из основной теоремы следует, что каждая конечная игра имеет цену. Цена игры v всегда лежит между нижней ценой игры а и верхней ценой игры Р:

Действительно, а есть максимальный гарантированный выигрыш, который мы можем себе обеспечить, применяя только свои чистые стратегии. Так как смешанные стратегии содержат в качестве частного случая все чистые, то, допуская кроме чистых еще и смешанные стратегии, мы, во всяком случае, не ухудшим своих возможностей; значит,

Аналогично, рассматривая возможности противника, докажем, что

откуда .

Предположим, что в игре нами найдено решение, состоящее из двух оптимальных стратегий:

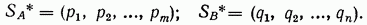
В общем случае, некоторые из чисел могут быть равными нулю, т. е. не все стратегии, доступные игроку, входят в его оптимальную смешанную стратегию. Будем называть активными стратегиями игрока те, которые входят в его оптимальную смешанную стратегию с отличными от нуля вероятностями. Для решения игр существенное значение имеет следующая теорема об активных стратегиях.

Если один из игроков придерживается своей оптимальной смешанной стратегии, то выигрыш остается неизменным и равным цене игры v, независимо от того, что делает другой игрок, если только тот не всходит за пределы своих активных стратегий (т. е. пользуется любой из них в чистом виде или смешивает их в любых пропорциях).

Докажем эту теорему. Пусть имеется решение игры в смешанных стратегиях, в котором некоторые стратегии являются активными, а другие нет. Перенумеруем стратегии так, чтобы активными были первые k стратегий игрока А и первые I стратегий игрока В. Решение будет иметь вид:

и его применение приводит к выигрышу, равному цене игры

Утверждается, что если мы (А) будем придерживаться своей стратегии то противник (В) может применять свои стратегии (но не ) в любых пропорциях; выигрыш при этом останется постоянным и равным

Обозначим выигрыш, образующийся, если мы пользуемся оптимальной стратегией а противник —чистыми стратегиями Из определения решения игры следует, что односторонее отклонение противника от его оптимальной стратегии не может быть ему выгодно; поэтому

14ЧТО НАЗЫВАЕТСЯ ПОЛЕЗНОЙ СТРАТЕГИЕЙ. Стратегия – это долгосрочное качественно определенное направление развития организации, касающееся сферы, средств и формы ее деятельности, системы взаимоотношений внутри организации, а также позиции организации в окружающей среде, приводящее организацию к ее целям.»

«Стратегия организации – это генеральный план действий, определяющий приоритеты стратегических задач, ресурсы и последовательность шагов по достижению стратегических целей.»

Date: 2016-05-25; view: 574; Нарушение авторских прав