Что называется седловой . Седловая точка матрицы- это элемент матрицы, который является максимальным в столбце и минимальным в строке. Точкойседловая точка. Чистая цена игры

Рассмотрим пример. Пусть дана матрица игры (4):

Требуется найти нижнюю цену игры α, верхнюю цену игры β и минимаксные стра­тегии и проверить, являются ли они устой­чивыми.

Решение. Из анализа дополнительных столбца и строки получаем: α= 5,β=5. Максимин равен минимаксу! Случай особый. Что же из этого следует?

Возьмем пару минимаксных стратегий: К ₂ и С ₃. Если оба держатся этих стратегий, то выигрыш будет равен 5. Теперь, допустим, мы узнали о поведении противника. Что будем делать? А ничего! Мы по-прежнему будем дер­жаться стратегии К ₂, потому что любое отступ­ление от нее нам невыгодно. Знаем мы или не знаем о поведении противника — все равно будем держаться стратегии К ₂! То же относится и к «синим» — им нет смысла менять свою стратегию С ₃.

В данном примере пара стратегий К ₂и С ₃устойчива, т. е. представляет собой положение равновесия и дает решение игры.

Почему так получилось? Потому что в матрице имеется особый элемент 5; он является минимальным в своей строке и одновременно максимальным в своем столбце. Такой элемент называется седловой точкой. Если матри­ца имеет седловую точку (т. е. нижняя цена игры равна верхней), то игра имеет решение в чистых стратегиях: это — пара стратегий, пересекающихся в седловой точке. Сама же седловая точка дает цену игры — в нашем примере она равна 5.

Класс игр, имеющих седловую точку, имеет большое значение в теории игр. В частности, доказано, что если по правилам игры каждый из игроков знает результат всех предыдущих ходов, как своих, так и противника (так на­зываемая игра с полной информацией), то игра имеет седловую точку и, значит, имеет решение в чистых стратегиях.

Примерами игр с полной информацией мо­гут служить: шахматы, шашки, «крестики и нолики» и т. п.

Приведем пример игры с полной информацией, решение которой легко найти.

Два игрока — К и С — поочередно кладут одинаковые монеты на круглый стол. Положение каждой монеты выбирается произвольно, лишь бы она не перекрывалась другими. Выигры­вает тот из игроков, который положит монету последним (когда места для других уже не остается).

Стоит немножко подумать, чтобы убедиться, что исход этой игры всегда предрешен и что существует вполне определенная стратегия, га­рантирующая выигрыш тому из игроков, кото­рый кладет монету первым (пусть это будет К). А именно К должен положить первую монету в центр стола, а далее на каждый ход С отвечать в точности симметричным относи­тельно центра стола ходом! Бедный С может при этом вести себя как угодно, спасения ему все равно нет...

Очевидно, такая игра имеет смысл только для тех, кто не знает решения. Любопытно, что совершенно так же обстоит дело и с такой популярной игрой, как шахматы! Эта игра име­ет смысл только до тех пор, пока не найдено ее решение.

Теоретически доказано, что решение су­ществует и исход шахматной игры в сущно­сти предрешен: если каждая сторона будет поль­зоваться своей оптимальной стратегией, то игра либо всегда будет кончаться выигрышем белых, либо всегда выигрышем черных, либо всегда ничьей! Но чем же именно? Мы пока этого не знаем, так как число возможных стра­тегий слишком велико, чтобы можно было построить матрицу шахматной игры и найти в ней седловую точку...

Наверное, любители шахмат заинтересованы в том, чтобы шахматная игра была решена еще не скоро.

Заметим в заключение, что седловых точек в матрице может быть не одна, а несколько; тог­да решений игры в чистых стратегиях суще­ствует столько, сколько имее

12ЧТО НАЗЫВАЕТСЯ СМЕШЕННОЙ СТРАТЕГИЕЙ. Игры, повторяемые многократно. Смешанные стратегии

Если партнеры играют только один раз, то игрокам целесообразно придерживаться принципа минимакса, как в игре с седловой точкой, так и в игре без седловой точки.

В случае многократного повторения игры с седловой точкой игрокам также целесообразно придерживаться принципа минимакса.

Если же многократно повторяется игра без седловой точки, то постоянное использование минимаксных стратегий становится невыгодным.

Действительно, в игре без седловой точки элемент платежной матрицы , соответствующий минимаксной стратегии игрока А, не обязан быть минимальным в своей строке. Следовательно, игрок В, зная о том, что игрок А в следующей игре будет использовать минимаксную стратегию 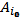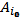, может выбрать стратегию, отвечающую минимальному элементу строки . В результате выигрыш игрока А уменьшится от величины , до величины . Аналогично может поступить и игрок А, неожиданно применив против игрока В стратегию, соответствующую максимальному элементу столбца .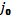

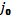Более того, доказано, что при многократно повторяемой игре без седловой точки игроку А, для обеспечения среднего выигрыша, большего, чем , следует чередовать свои стратегии . Игроку В для улучшения результата также целесообразно чередовать свои стратегии .

По этой причине для многократно повторяемых игр без седловой точки вводится следующее определение.

• В играх, которые повторяются многократно, каждая из стратегий называется чистой стратегией.
• Стратегия игрока А, обозначаемая

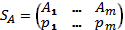
и состоящая в том, чтобы применять чистые стратегии , чередуя их по случайному закону с частотами 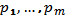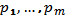, называется смешанной стратегией. Частоты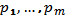 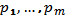удовлетворяют соотношению

.

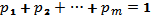
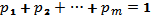• Чистые и смешанные стратегии игрока В определяются аналогично.

Замечание. Каждая чистая стратегия является частным случаем смешанной стратегии, когда одна из стратегий применяется с частотой 1, а все остальные – с частотой 0.

• Смешанные стратегии, избранные игроками, называются оптимальными, если одностороннее отклонение любым игроком от своей оптимальной стратегии может изменить средний выигрыш только в сторону, невыгодную для этого игрока.
• Совокупность, состоящая из оптимальной стратегии одного игрока и оптимальной стратегии другого игрока, называется решением игры.
• Средний выигрыш V при применении обоими игроками оптимальных стратегий называется ценой игры.
• Стратегии, входящие с ненулевыми частотами в оптимальную стратегию игрока, называются полезными.

В 1928 году фон Нейманом была доказана основная теорема теории игр, утверждающая, что каждая игра имеет, по крайней мере, одно решение, возможно, в области смешанных стратегий.

Поскольку все чистые стратегии являются частными случаями смешанных стратегий, то из основной теоремы теории игр можно получить

Следствие 1. Любая игра имеет цену.

Следствие 2. Цена игры удовлетворяет неравенству .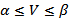

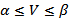Следствие 3. Средний выигрыш остается равным цене игры, если один из игроков придерживается своей оптимальной стратегии, а другой игрок применяет свои полезные стратегии с любыми частотами.

Date: 2016-05-25; view: 1436; Нарушение авторских прав