Классическая и уточненная теория изгиба прямоугольных пластин

Рассмотрим пластину в декартовой системе координат (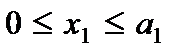, , 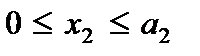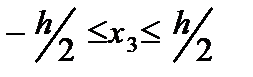), где 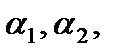h - размеры пластины вдоль координатных осей). Будем излагать одновременно две теории: классическую (слева) и уточненную (справа). Эти теории основаны на следующих гипотезах:

1. Линейная деформация в поперечном направлении (обжатие) отсутствует

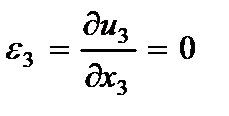
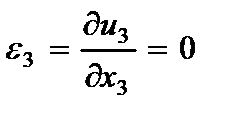(2.99)

где 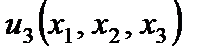- перемещение по оси ;

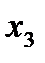2. Сдвиговые деформации в перпендикулярных плоскостях пластины изменяются по заданным законам

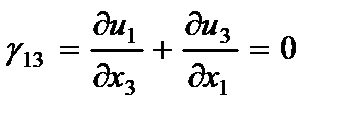
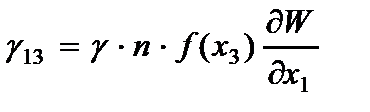
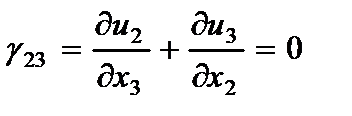
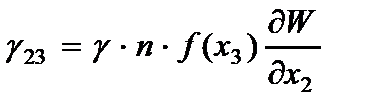(2.100)

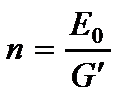
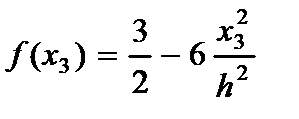
где 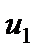, 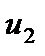- перемещения по осям 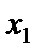, 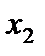соответственно; 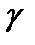- параметр поперечного сдвига; 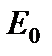- обобщенный модуль упругости; 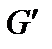- модуль сдвига материала пластины; 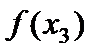- функция распределения поперечных сдвигов.

3. Нормальное напряжение по оси 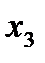(давление слоев) отсутствует

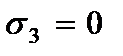
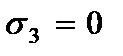(2.101)

4. Горизонтальная плоскость пластины (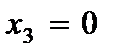) не испытывает деформацию растяжения (сжатия)

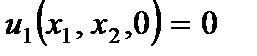
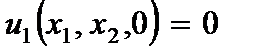(2.102)

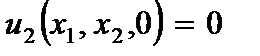
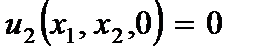
Принятые гипотезы позволяют свести трехмерную задачу к двухмерной.

Интегрируя (2.63), (2.64) и учитывая при этом (2.66) имеем компоненты перемещений

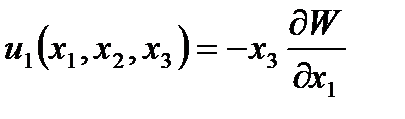
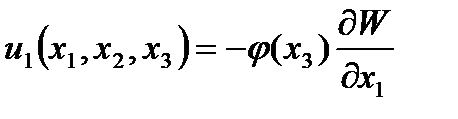
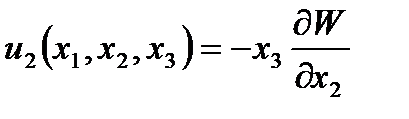
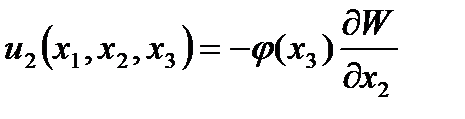(2.103)

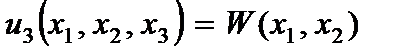
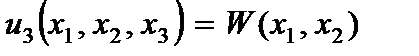
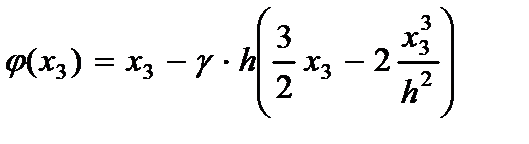
где 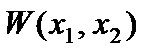- функция прогибов пластины; 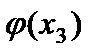- функция распределения тангенциальных перемещений.

На основании (2.63) определяются компоненты деформации

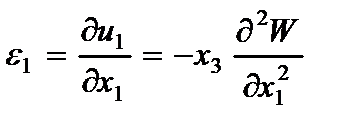
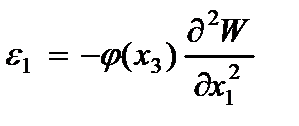
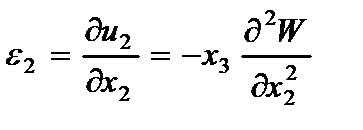
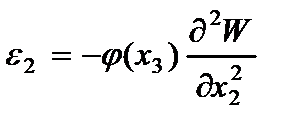
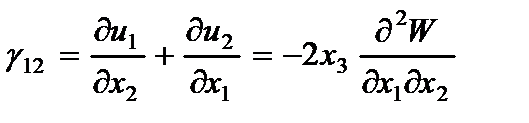
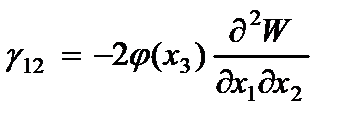
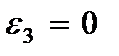
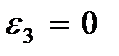(2.104)

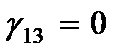
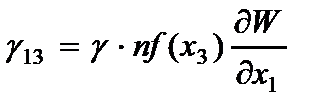
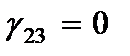
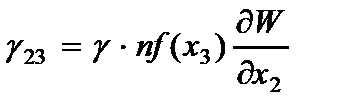
Компоненты напряжений, вычисленные по обобщенному закону Гука с учетом гипотезы (2.61) имеют вид

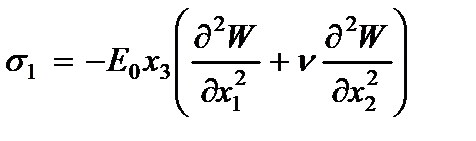
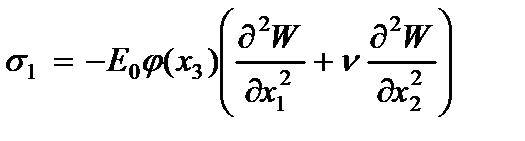
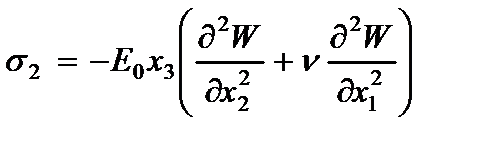
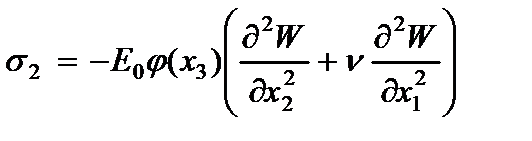
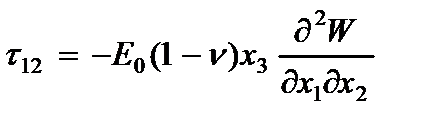
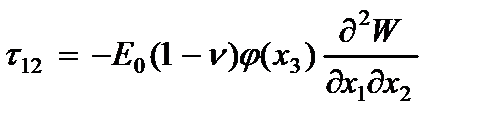
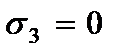
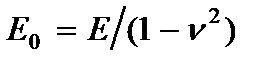
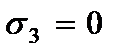
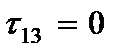
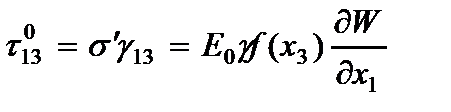
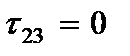
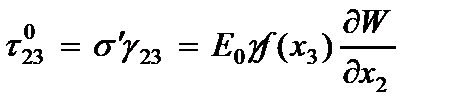
где 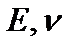- модуль упругости и коэффициент Пуассона материала пластины.

Поперечные касательные напряжения, полученные интегрированием уравнений равновесия в напряжениях

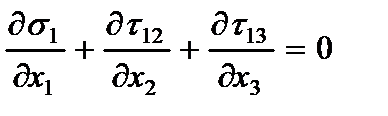
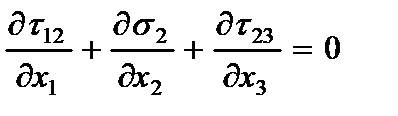
с учетом напряжений (2.6) и граничных условий при 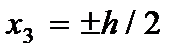, равны

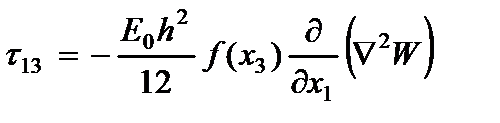
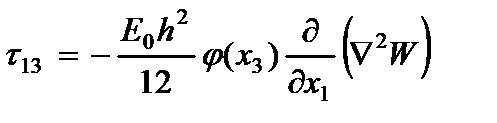
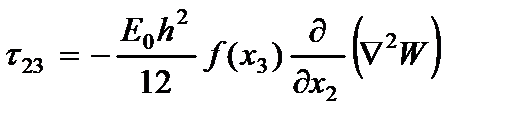
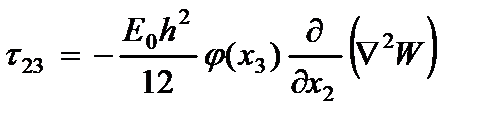(2.105)

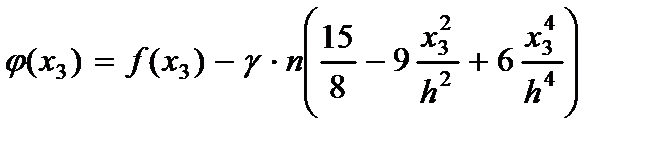
где 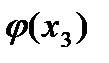- функция распределения поперечных касательных напряжений; 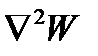- оператор Лапласа.

Внося их в уравнение равновесия в напряжениях

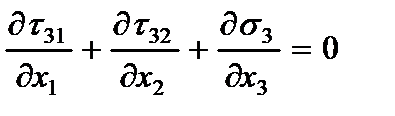
и интегрируя его с учетом граничного условия 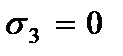при 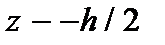, получим выражения для

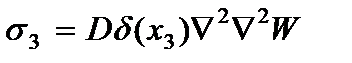
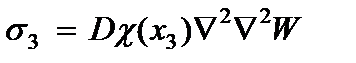
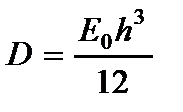
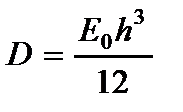(2.106)

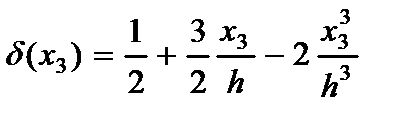
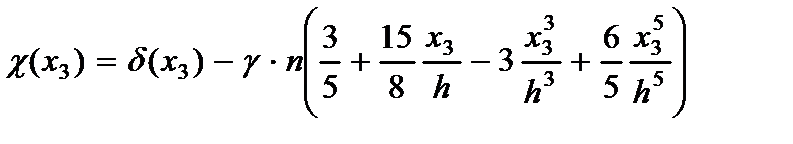
где 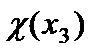- функция распределения поперечных нормальных напряжений; 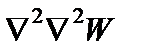- бигармонический оператор.

Разрешающее уравнение для определения функции прогибов вытекает из условия 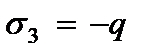, при 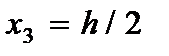с учетом (2.106)

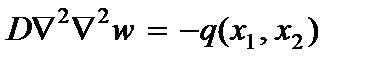
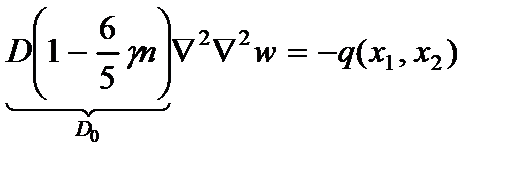(2.107)

где 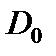- обобщенная цилиндрическая жесткость пластины.

Определим интегральные характеристики

· Перемещений (2.103)

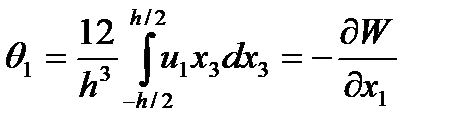
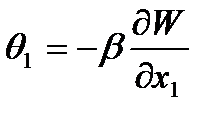
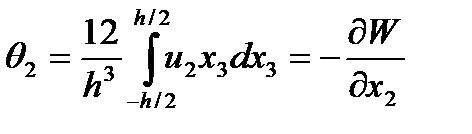
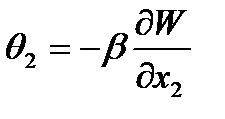(2.108)

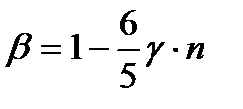
где 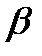- параметр цилиндрической жесткости;

· Напряжений(2.104) и (2.105)

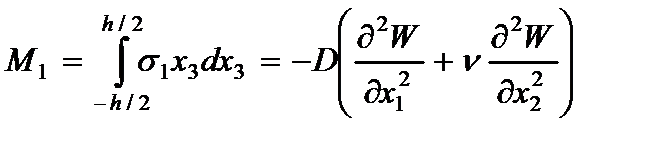
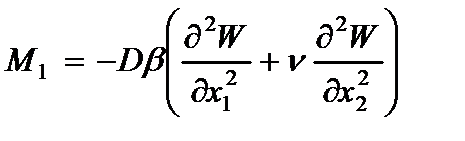
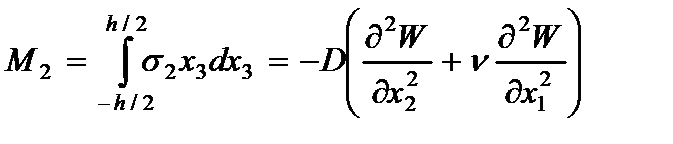
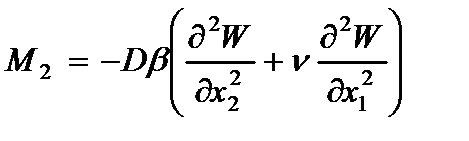(2.109)

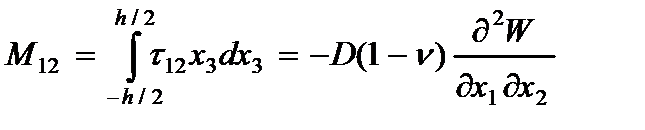
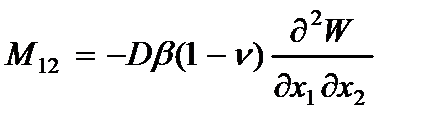
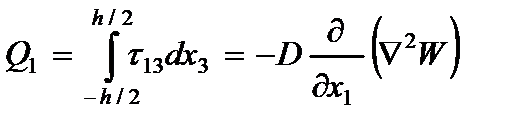
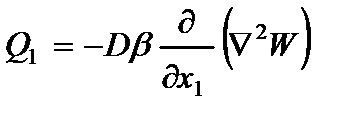
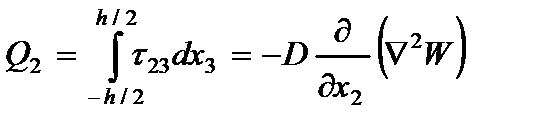
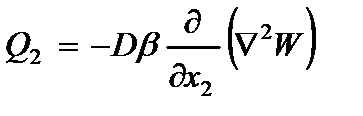
где 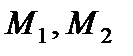- изгибающие моменты; 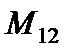- крутящий момент; 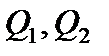- поперечные силы.

На основании их представим

· Перемещений (2.103)

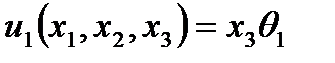
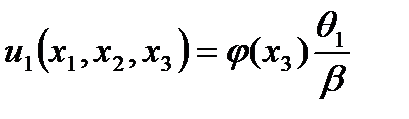
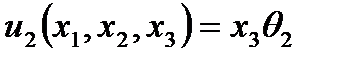
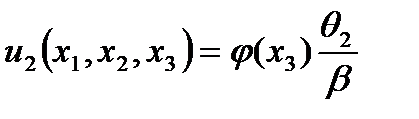(2.110)

· Напряжений (2.104), (2.105) и (2.106)

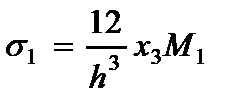
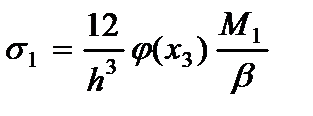
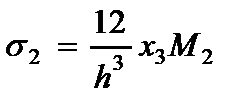
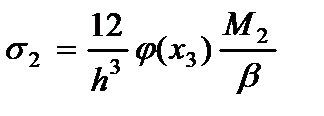
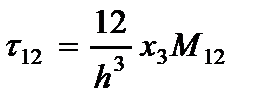
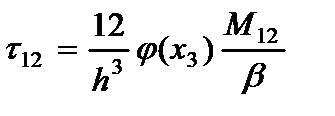(2.111)

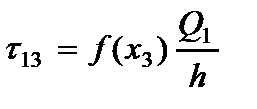
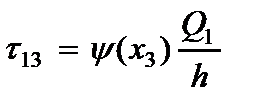
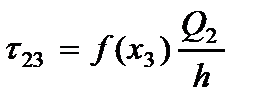
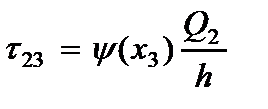
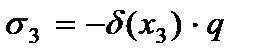
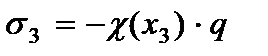
Граничные условия для края пластины 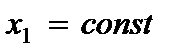вытекают из условия равновесия пластины

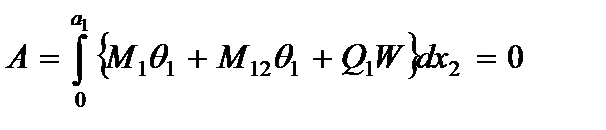(2.112)

где А – полная работа контурных условий.

Для определения параметра поперечного сдвига 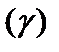определим поперечные силы с использованием напряжений (2.104)

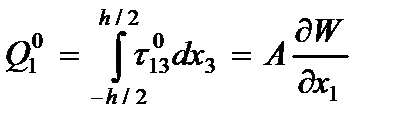
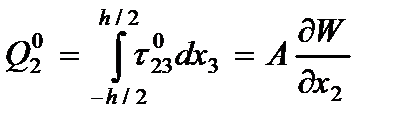(2.113)

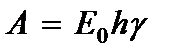
где А – жесткость пластины при поперечном сдвиге.

Равенство поперечных сил (2.109) и (2.113) будут выполняться при следующих условиях

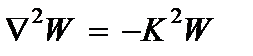
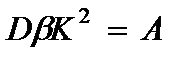, (2.114)

где первое уравнение (уравнение свободных колебаний мембраны), предназначено для определения параметра .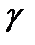

Учитывая (2.108) и (2.113) из (2.114) имеем

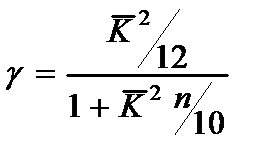
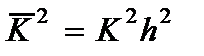, (2.115)

следовательно параметр 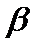(2.108) имеет вид

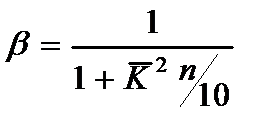(2.116)

Решение первого уравнения (2.114) представим в виде

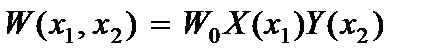(2.117)

где 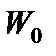- максимальный прогиб мембраны; 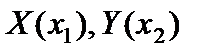- известные балочные функции.

На основании (2.117) уравнение свободных колебаний мембраны имеет вид

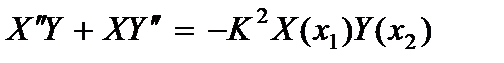
Разделяя переменные, запишем его в виде

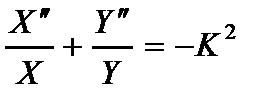(2.118)

При выполнении следующих уравнений

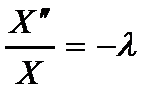
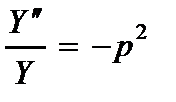(2.119)

где первое и второе уравнение устойчивости стержней, направленных вдоль координатных осей 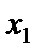и .

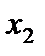На основании (2.119) собственное число мембраны (2.118) равно

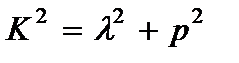(2.120)

Приведем результаты решения первого уравнения (2.119) для случаев:

1. Концы стержня шарнирно оперты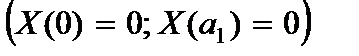

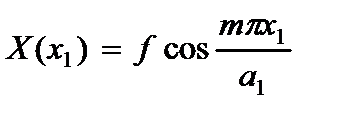
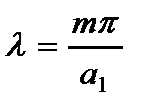(2.121)

2. Один конец защемлен, другой свободен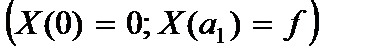

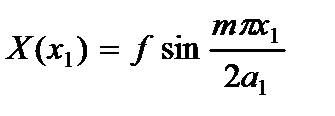
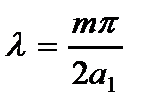(2.122)

3. Концы стержня защемлены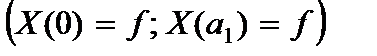

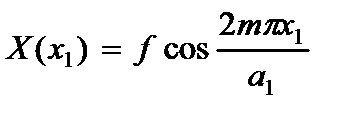
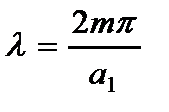(2.123)

Варьируя результаты (2.121)-(2.123) можно найти по формуле (2.120) результаты для мембраны, совпадающей с пластиной. Так

1. для пластины шарнирно опертой по контуру

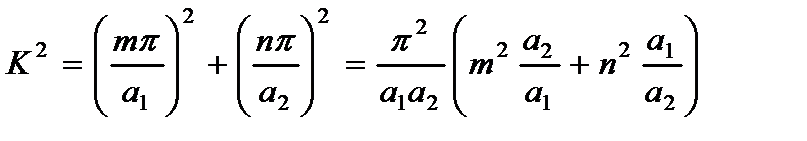(2.124)

где 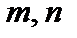- волновые числа вдоль осе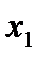й и ;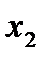

2. для пластины, шарнирно опертой по сторонам 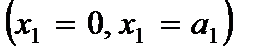и защемленной по сторонам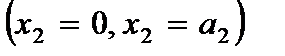

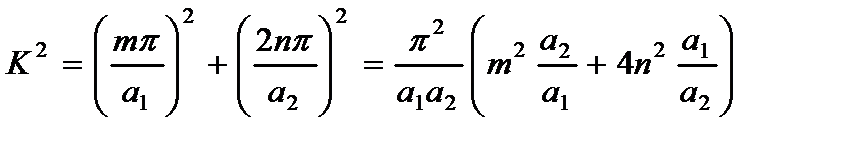(2.125)

3. для пластины при выполнении условий (2.122) для сторон 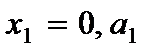и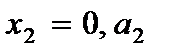

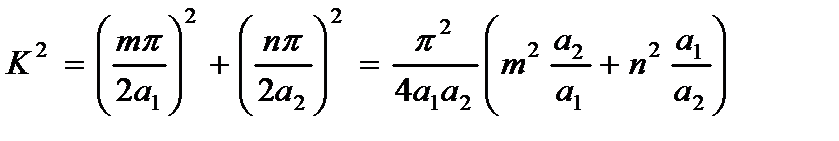(2.126)

Аналогичным образом можно получить результаты для параметра 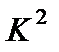при других граничных условиях.

Таким образом, предложенная уточненная теория пластины позволяет легко учесть поперечные сдвиги по классической теории пластин с введением только параметра поперечного сдвига.

Date: 2016-05-24; view: 788; Нарушение авторских прав