Прямоугольная пластинка. Решение Леви

Решение Л. Навье, рассмотренное в предыдущем параграфе, пригодно только для прямоугольных пластинок, шарнирно опертых по контуру. Более общим является решение М. Леви. Оно пригодно для прямоугольной пластинки, два противоположных края которой шарнирно оперты, а два других имеют любое закрепление (защемление, шарнирное опирание) или свободны.

Рис. 1.9

У пластинки, изображенной на рис. 1.9, шарнирно опертыми являются края OC и AB. Граничные условия на этих краях таковы:

При x = 0 и x = a 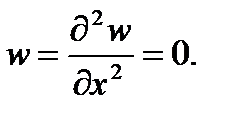(а)

Чтобы выполнить эти условия, функцию прогибов можно взять в виде

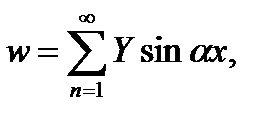(б)

где Y – произвольная функция одного аргумента y; α = nπ/a.

Так как при x = 0 и x = a sin αx = 0, то функция (б) удовлетворяет условиям (а) в отношении прогибов. Чтобы проверить условия (а) для изгибающих моментов, подсчитываем вторые частные производные функции прогибов (б) по x и y:

(в)

При x = 0 и x = a эти производные, аналогично самой функции, обращаются в нуль и, следовательно, условия (а) в отношении изгибающих моментов также выполняются.

Функция (б) должна удовлетворять основному уравнению изгтиба пластинки. Подставляя ее четвертые производные в уравнение (1.18), получаем

(г)

Для решения уравнения (г) разложим его правую часть в тригонометрический ряд Фурье по синусам:

(д)

Коэффициенты ряда Фурье F_n (y) являются здесь функцией y. Так как разложение производится на отрезке 0 ≤ x ≤ a, то их определяют по формуле

(е)

Подставим ряд (д) в уравнение (г):

Вынося знак суммирования за скобки, получим

Это условие выполняется, если каждый член ряда равен нулю:

(ж)

Решение однородного дифференциального уравнения четвертого порядка (ж) равно сумме общего решения соответствующего однородного уравнения и какого-нибудь частного решения неоднородного уравнения. Однородное уравнение имеет вид

(з)

Его решение можно представить так:

(и)

Обозначив частное решение уравнения (ж), получим его общее решение:

(к)

Подставляя функцию Y (y) в формулу (б), находим

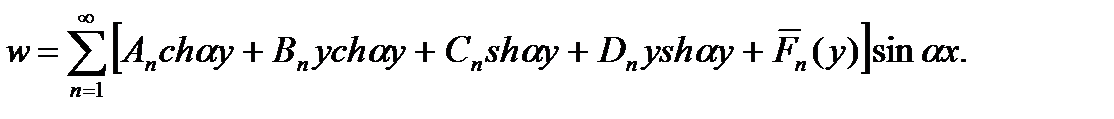(л)

Функция w является решением уравнения (1.18) в случае поперечной нагрузки q (x, y), распределенной на поверхности пластинки по любому закону, и, как показано выше, удовлетворяет граничным условиям на шарнирно опертых краях OC и AB.

Рассмотрим построение частного решения . Согласно правилу Коши, частное решение неоднородного дифференциального уравнения четвертого порядка выражается интегралом

(м)

где F_n (t) – правая часть решаемого уравнения, которая определяется выражением (е) при замене аргумента y на t, а ψ (y) – частное решение соответствующего однородного уравнения. Оно удовлетворяет условиям

(о)

Заменив в функциях (о) и (е) аргументы и подставив эти функции в формулу (м), получим искомое частное решение уравнения (ж):

Для определения произвольных постоянных A_n, B_n, C_n и D_n используем граничные условия на краях OA и BC. Рассмотрим пластинку, у которой эти края жестко защемлены (см. рис. 1.9). Тогда имеем следующие граничные условия:

при y = 0 и y = b

Подставив в них функцию прогибов (б), получим:

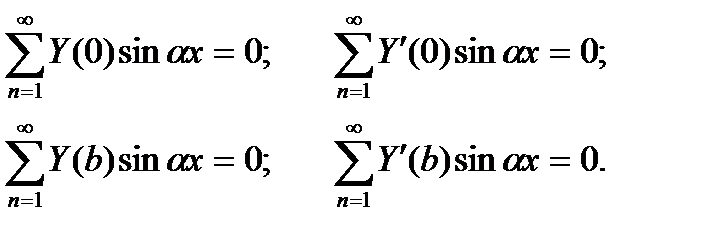
Так как эти условия должны выполняться при любых значениях аргументы x, то

(п)

Внося в условия (п) функцию (к), получим систему уравнений для определения постоянных:

откуда

A_n = 0;

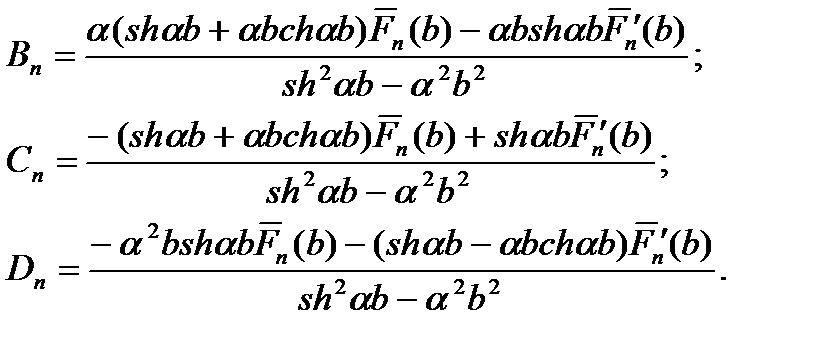
При других закреплениях краев OA и BC получаются другие значения постоянных.

Ряды в функции прогибов и ее производных сходятся значительно быстрее, чем тригонометрические ряды в решении Л. Навье, поэтому решение М. Леви более удобно в практических расчетах даже для прямоугольной пластинки, шарнирно опертых по всему контуру.

Date: 2016-05-24; view: 3103; Нарушение авторских прав