Прямоугольная пластинка. Решение Навье

Решение основного уравнения изгиба (1.18) для прямоугольной пластинки в замкнутой форме получить не удастся. Его приходится искать в виде бесконечного ряда. Рассмотрим шарнирно опертую по контуру прямоугольную пластинку (рис. 1.8), находящуюся под действием поперечной нагрузки интенсивностью q (x, y), изменяющейся по любому закону. Начало координат расположим в углу пластинки. Размер пластинки в направлении оси x равен a, а в направлении оси y – b.

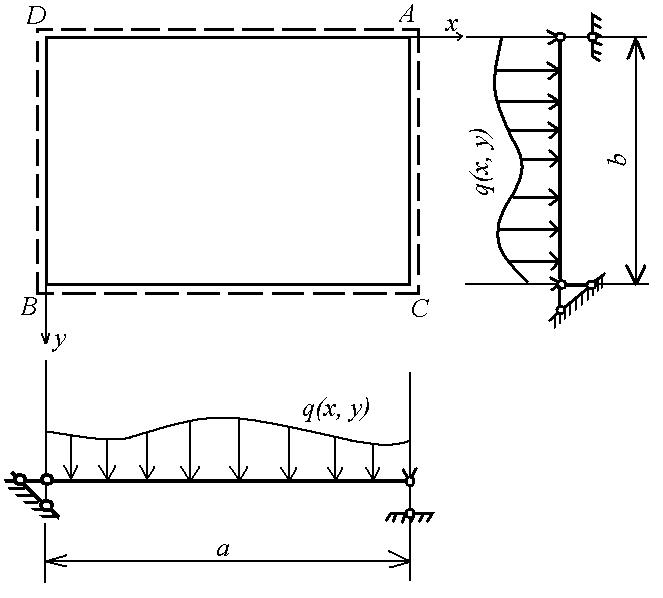
Рис. 1.8

Решение уравнения (1.18) будем искать в виде двойного тригонометрического ряда по синусам:

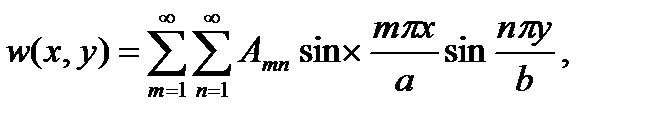(а)

где A_mn – постоянные числа, коэффициенты ряда; m и n – целые положительные числа: 1, 2, 3 …

Ряд (а) можно представить в развернутом виде:

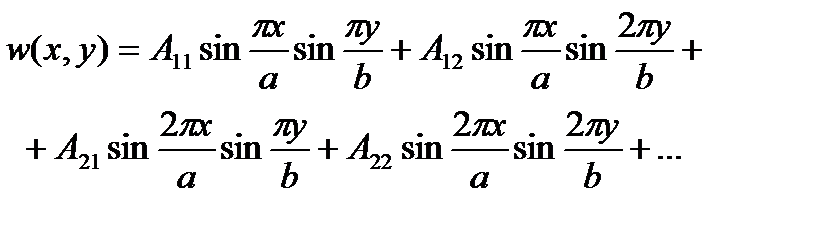
Для шарнирно опертой по контуру пластинки имеем следующие граничные условия:

при x = 0 и x = a 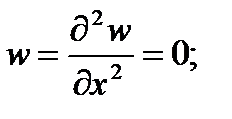(б)

при y = 0 и y = b 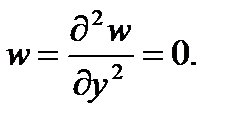(в)

Убедимся, что ряд (а) удовлетворяет этим условиям. Действительно, на грани пластинки x = 0 и, следовательно, прогиб w (0, y) = 0. На грани x = a 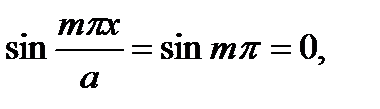а значит, прогиб w (a, y) = 0. Точно так же обращаются в нуль прогибы на гранях y= 0 и y=b. Следовательно, граничные условия (б) и (в) в отношении прогибов выполняются.

Вторые производные функции прогибов

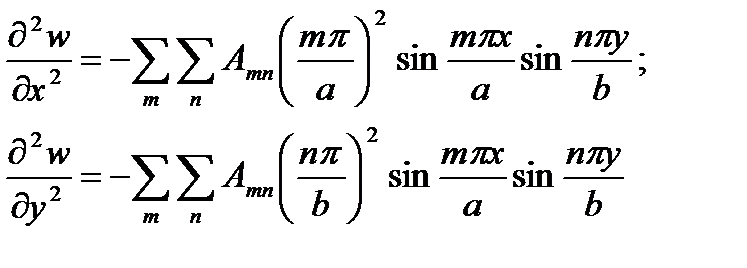
содержат синусы тех же аргументов, что и сама функция. Поэтому производные обращаются в нуль на всех гранях пластинки: при x = 0, x = a, y= 0 и y=b. Следовательно, граничные условия (б) и (в) для изгибающих моментов также выполняются.

Определим коэффициенты ряда (а). Для этого подсчитаем четвертые производные функции прогибов

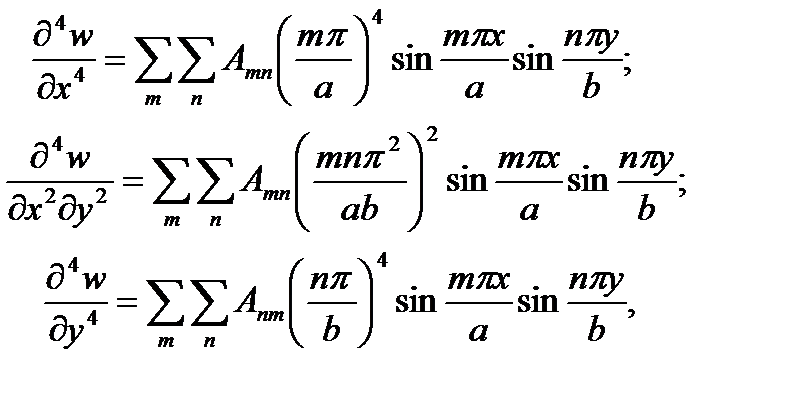
подставив их в уравнение (1.18), после упрощения получим

(г)

Чтобы определить коэффициенты ряда, входящего в левую часть уравнения (г), необходимо и правую часть этого уравнения разложить в тригонометрический ряд. Представим нагрузку в виде двойного тригонометрического ряда Фурье по синусам в прямоугольной области 0 ≤ x ≤ a; 0 ≤ y ≤ b:

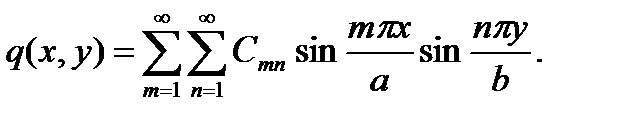(д)

Коэффициенты этого ряда определяются по формуле, известной из курса математического анализа:

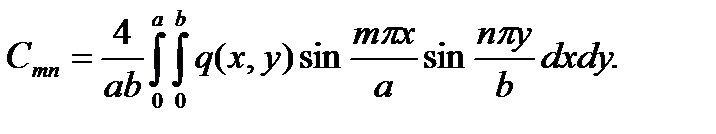(е)

Подставив ряд (д) в уравнение (г), получим

Два ряда равны между собой, если равны их соответствующие члены. Таким образом,

Подставляя сюда вместо C_mn выражение (е), находим коэффициенты ряда (а) в такой форме:

(ж)

Функция (а) является решением поставленной задачи, так как она удовлетворяет условиям на контуре пластинки и при выборе коэффициентов ряда в форме (ж) удовлетворяет основному уравнению изгиба пластинки. Дальнейшая конкретизация задачи зависит от вида функции q (x, y).

Date: 2016-05-24; view: 3534; Нарушение авторских прав