
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

В уточненной постановке
|
|

Рассмотрим однородную трансверсально изотропную пластину, отнесенную к декартовой системе координат (рис.1).
Рис.1 Прямоугольная пластина
Принимаем следующие гипотезы:
1. Материал пластины в направлении оси  не обжимает и не испытывает давления
не обжимает и не испытывает давления
 ;
;  . (2.1)
. (2.1)
2. Поперечные сдвиговые деформации изменяются по заданному закону
 , (1.2);
, (1.2);
 ;
;  , (2.2)
, (2.2)
где (1.2) – символ, означающий перестановку индексов для получения другого выражения из заданного;  - безразмерная поперечная координата;
- безразмерная поперечная координата;  - толщина пластины;
- толщина пластины;  - углы сдвигов;
- углы сдвигов;  - закон изменения сдвигов по толщине пластины.
- закон изменения сдвигов по толщине пластины.
Считая, что мембранные деформации срединной поверхности пластины отсутствуют, из выражений деформации  и
и  определяем компоненты перемещений:
определяем компоненты перемещений:
 ; (2.3)
; (2.3)
 (1.2);
(1.2);
 .
.
Здесь  – частная производная по координате
– частная производная по координате  от прогибов пластины
от прогибов пластины  ;
;  - закон изменения тангенциальных перемещений по толщине пластины при учете поперечных сдвигов.
- закон изменения тангенциальных перемещений по толщине пластины при учете поперечных сдвигов.
Используя закон Гука и (2.3), находим компоненты напряжений:
 (1.2);
(1.2);
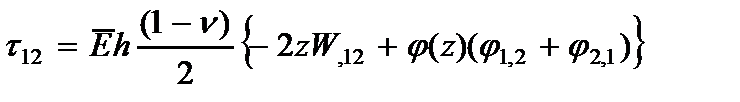 , (2.4)
, (2.4)
 (1.2);
(1.2);
 .
.
Им будут соответствовать следующие внутренние усилия:
 (1.2)
(1.2)
 (2.5)
(2.5)
 (1.2);
(1.2);
Жесткости пластины при сдвиге  и изгибе
и изгибе  равны:
равны:

 (2.6)
(2.6)
 .
.
Интегрируя по толщине пластины уравнения теории упругости в напряжениях
 (1.2);
(1.2);
 (2.7)
(2.7)
и учитывая граничные условия на поверхностях
при  :
: 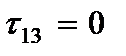 (1.2)
(1.2)
при  :
:  ;
;
при  :
:  , (2.8)
, (2.8)
получим систему уравнений в усилиях
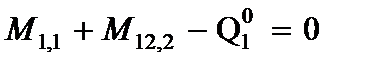 (1.2)
(1.2)
 . (2.9)
. (2.9)
Внося значения усилий (2.5) в (2.9) имеем систему разрешающих уравнений, полученную С.А. Амбарцумяном [1] относительно искомых функций ( ):
):
 (1.2);
(1.2);
 . (2.10)
. (2.10)
Чтобы сформулировать граничные условия задачи поперечного изгиба рассмотрим контурный интеграл для края пластины х1=const
 . (2.11)
. (2.11)
Внося значения перемещений (2.3) в (2.11) и учитывая обозначения
 ;
;  (2.12)
(2.12)
представим его в виде:
 . (2.13)
. (2.13)
При этом обобщенные моменты (2.12) с учетом (2.4) определяются выражениями
 (1.2);
(1.2);
 . (2.14)
. (2.14)
Принимая 17/168»1/10 выразим обобщенные моменты через обычные
 ;
;  . (2.15)
. (2.15)
С учетом (2.15) контурный интеграл (2.13) представится в виде:
 . (2.16)
. (2.16)
Определим осредненные углы поворотов поперечных сечений пластины с учетом (2.3) по формулам:
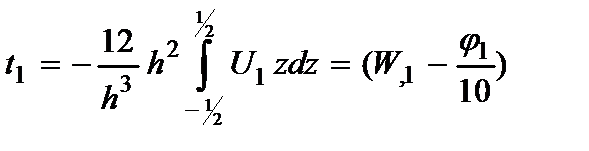 (1.2). (2.17)
(1.2). (2.17)
Тогда контурный интеграл (2.16) выразится через основные характеристики пластин ( ):
):
 . (2.18)
. (2.18)
Приравнивая (2.18) к нулю, получим различные варианты граничных условий моделирующих крепления пластины по контуру.
Решение системы уравнений (2.10) с краевыми условиями (2.18) получено для ограниченного класса задач. В общем случае его получить невозможно.
Рассмотрим варианты уравнений, вытекающие из системы (2.10).
Первый вариант. Продифференцируем первое уравнение системы (2.10) по координате х1, а второе – по х2 и сложим их. В результате с учетом последнего уравнения из (2.10), получим уравнения теории типа Тимошенко [3]:
 . (2.19)
. (2.19)
Если же продифференцировать первое уравнение из (2.10) по координате х2, а второе – по х1 и вычесть из первого выражения второе, то получим уравнение, описывающее краевой эффект Рейсснера [14]:
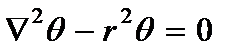 ;
;
 ; (2.20)
; (2.20)
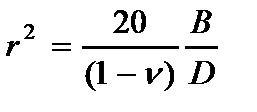 .
.
Последнее уравнение системы (2.10) запишем в виде:
 ;
; 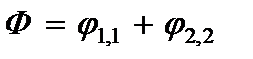 . (2.21)
. (2.21)
Таким образом, система уравнений (2.10) эквивалентна трем уравнениям (2.19) - (2.21).
Чтобы определить углы сдвигов ( ), определяем поперечные силы из первых двух уравнений системы (2.10)
), определяем поперечные силы из первых двух уравнений системы (2.10)
 ;
;
 . (2.22)
. (2.22)
Приравнивая поперечные силы ( ) и (
) и ( ), находим углы сдвигов
), находим углы сдвигов
 ;
;  , (2.23)
, (2.23)
где  вычисляются по (2.22).
вычисляются по (2.22).
Внутренние усилия (2.5) для данного варианта имеют вид:
 ;
;
 ;
;
 ;
;
 ;
;  . (2.24)
. (2.24)
Отметим, что уравнение (2.21) превращается в уравнение (2.19) если вычислить значение функции  , используя (2.23), следовательно, независимыми уравнениями для рассматриваемого варианта будут (2.20) и (2.19). Этим уравнениям соответствует контурный интеграл (2.16) при вычислении углов сдвигов по формуле (2.23).
, используя (2.23), следовательно, независимыми уравнениями для рассматриваемого варианта будут (2.20) и (2.19). Этим уравнениям соответствует контурный интеграл (2.16) при вычислении углов сдвигов по формуле (2.23).
Таким образом, путем преобразования система разрешающих уравнений (2.10) приводится к двум разрешающим уравнениям (2.19), (2.20) с общим порядком равным шести относительно двух функций ( ).
).
Достоинством данного подхода является то, что разрешающие уравнения оказались не связанными, а недостатком – функции  и
и  оказались связанными в граничных условиях.
оказались связанными в граничных условиях.
Второй вариант. Пусть углы сдвигов выражены через функцию 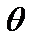 (2.20) следующим образом:
(2.20) следующим образом:
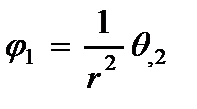 ;
;  , (2.25)
, (2.25)
где параметр  вычисляется по (2.20).
вычисляется по (2.20).
На основании (2.25) находим функцию  по (2.20)
по (2.20)
 . (2.26)
. (2.26)
и функцию  по (2.21)
по (2.21)
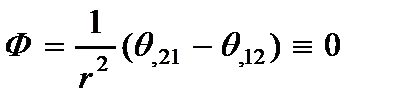 . (2.27)
. (2.27)
Представление вида (2.25) правомерное, так как из выражения функции  получается разрешающее уравнение (2.20).
получается разрешающее уравнение (2.20).
Внося (2.27) в (2.21), получим  , следовательно, разрешающее уравнение (2.19) имеет вид:
, следовательно, разрешающее уравнение (2.19) имеет вид:
 . (2.28)
. (2.28)
Внося (2.25) в (2.24) получим значение внутренних усилий:
 ;
;
 ;
;
 ;
;
 ;
;  . (2.29)
. (2.29)
Контурный интеграл (16) запишется в виде:
 . (2.30)
. (2.30)
Таким образом, путем подстановки (2.25) система разрешающих уравнений (2.10) приводится к двум независимым между собой уравнениям (2.26) и (2.28) с граничными условиями (2.30), описывающими поперечный изгиб с учетом только контурных усилий. Следует отметить, что функция  появляется только в том случае, когда на пластину действуют контурные нагрузки, т.е. она описывает краевой эффект пластины, поэтому данный вариант используется для ограниченного класса задач. Например, при расчете полубесконечной пластины.
появляется только в том случае, когда на пластину действуют контурные нагрузки, т.е. она описывает краевой эффект пластины, поэтому данный вариант используется для ограниченного класса задач. Например, при расчете полубесконечной пластины.
Третий вариант. В научной литературе широко используется метод подстановок для решения дифференциальных уравнений. Так, например, следуя [6] выразим углы поворотов (2.17) через новые функции  и
и  :
:
 ;
;  . (2.31)
. (2.31)
Тогда система уравнений (2.10) преобразуется к виду:
 ;
;
 ; (2.32)
; (2.32)
 .
.
Мы пришли к системе уравнений, в той или иной форме неоднократно обсуждавшейся в научной литературе [2,10,11,12,13].
Внутренние усилия (5) запишутся так:
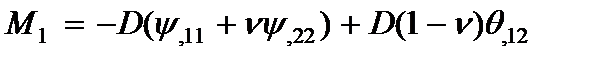 ;
;
 ;
;
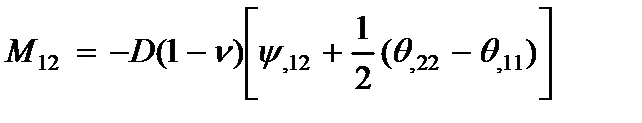 ;
;
 ;
;  . (2.33)
. (2.33)
Граничный интеграл будет определяться по (2.16) с учетом (2.31). Систему (2.32) можно представить в такой форме:
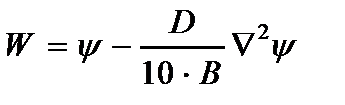 ;
;
 ; (2.34)
; (2.34)
 .
.
Такая форма представления разрешающей системы использована в расчетах трехслойных пластин в монографии [4]. При  она же использована в работе [5].
она же использована в работе [5].
Достоинством данного варианта является то, что система разрешающих уравнений (2.10) приводится к двум уравнениям относительно функции  и
и  . Причем, при
. Причем, при  для решения ограниченного класса задач можно использовать аппарат классической теории пластин. Поперечные силы, определенные из уравнений равновесия, которые входят в контурный интеграл вместо поперечных сил
для решения ограниченного класса задач можно использовать аппарат классической теории пластин. Поперечные силы, определенные из уравнений равновесия, которые входят в контурный интеграл вместо поперечных сил 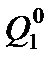 и
и  имеют вид:
имеют вид:
 ;
;
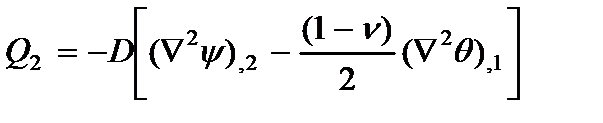 . (2.35)
. (2.35)
При  , т.е. когда краевой эффект не учитывается контурный интеграл (2.18) запишется с учетом (2.31) и (2.34) в виде:
, т.е. когда краевой эффект не учитывается контурный интеграл (2.18) запишется с учетом (2.31) и (2.34) в виде:
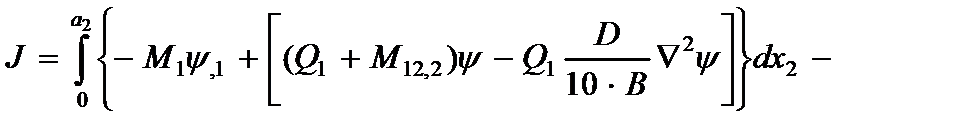
 . (2.36)
. (2.36)
Отсюда видно, что решение уравнения (2.34) при  осуществляется достаточно просто для ограниченного класса задач, главным образом, для шарнирно-опертых пластин. Задача значительно усложняется для других, более сложных случаев опирания.
осуществляется достаточно просто для ограниченного класса задач, главным образом, для шарнирно-опертых пластин. Задача значительно усложняется для других, более сложных случаев опирания.
Четвертый вариант. В предыдущем варианте осредненные углы поворотов поперечных сечений пластин были выражены через две новые функции. В данном варианте углы сдвигов  и
и  выразим через них:
выразим через них:
 ;
;  . (2.37)
. (2.37)
Тогда система (2.10) приводится к виду:
 ;
;
 ; (2.38)
; (2.38)
 ,
,
где коэффициент  определяется по-прежнему по (2.20).
определяется по-прежнему по (2.20).
Будем считать  , т.е. пластина загружена только поперечной нагрузкой (нагрузки, приложенные по контуру, отсутствуют). Взяв, оператор Лапласа от обеих частей второго уравнения с учетом третьего уравнения системы (2.38), представим систему, полученную А.Ф.Рябовым [8], (2.38) в виде:
, т.е. пластина загружена только поперечной нагрузкой (нагрузки, приложенные по контуру, отсутствуют). Взяв, оператор Лапласа от обеих частей второго уравнения с учетом третьего уравнения системы (2.38), представим систему, полученную А.Ф.Рябовым [8], (2.38) в виде:
 ,
,
 (2.39)
(2.39)
Внутренние усилия (2.5) с учетом (2.37) при 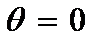 имеют вид:
имеют вид:
 ,
,
 ,
,
 . (2.40)
. (2.40)
Контурный интеграл (2.16) с учетом (2.37) запишется следующим образом:

 . (2.41)
. (2.41)
В этом случае удается выделить функцию  , т.е. она не связана с функцией не только в уравнениях, но и в граничных условиях. Расчет пластины при использовании данного варианта производится следующим образом. Вначале решается второе уравнение из (2.39) с использованием граничных условий
, т.е. она не связана с функцией не только в уравнениях, но и в граничных условиях. Расчет пластины при использовании данного варианта производится следующим образом. Вначале решается второе уравнение из (2.39) с использованием граничных условий  . В результате находится функция
. В результате находится функция  , которая используется при решении первого уравнения из (2.39) с граничными условиями из (2.41).
, которая используется при решении первого уравнения из (2.39) с граничными условиями из (2.41).
К достоинствам данного варианта можно отнести тот факт, что использование системы (2.39) позволяет расширить круг решаемых задач.
Пятый вариант. Если принять, что углы сдвигов представимы в форме:
 ;
;  , (2.42)
, (2.42)
где функции  и
и  удовлетворяют условию
удовлетворяют условию  , то система (2.10) приводится к виду (2.38) при
, то система (2.10) приводится к виду (2.38) при  .
.
Взяв оператор Лапласа от обеих частей второго уравнения системы (2.38) и изменяя  через нагрузку
через нагрузку  приходим к следующей системе уравнений, полученной В.В. Пикулем [7]:
приходим к следующей системе уравнений, полученной В.В. Пикулем [7]:
 ,
,
 . (2.43)
. (2.43)
Внутренние усилия определяются по (2.40) и имеют вид:
 (1.2);
(1.2);
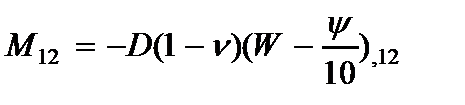
 . (2.44)
. (2.44)
При определении  использовано второе уравнение из (2.38).
использовано второе уравнение из (2.38).
Контурный интеграл остается без изменения, т.е. определяется по (2.41).
Достоинством данного варианта является то, что функции  и
и  не связанные только в уравнениях, но и в граничных условиях, причем для решения первого уравнения из (2.43) можно использовать аппарат классической теории пластин. После того, как находятся искомые функции из выражения функции
не связанные только в уравнениях, но и в граничных условиях, причем для решения первого уравнения из (2.43) можно использовать аппарат классической теории пластин. После того, как находятся искомые функции из выражения функции  , вычисляется функция прогибов
, вычисляется функция прогибов  .
.
Шестой вариант. В основу данного варианта положена система (2.38), которая получена из системы (2.10) при использовании подстановки (2.37).
Анализ системы (2.38) показывает, что второе уравнение связывает функцию  с функцией
с функцией 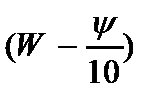 , а последнее уравнение этой же системы – функцию
, а последнее уравнение этой же системы – функцию  с поперечной нагрузкой
с поперечной нагрузкой  . При
. При  , если функцию
, если функцию 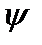 со второго уравнения подставить в третье уравнение, то система (2.38) преобразуется к виду:
со второго уравнения подставить в третье уравнение, то система (2.38) преобразуется к виду:
 , (2.45)
, (2.45)
 . (2.46)
. (2.46)
Структура дифференциальной зависимости (2.45) такова, что левая часть соответствует чисто сдвиговому состоянию пластины, а правая – состоянию при совместном действии сдвига и изгиба. Ее назначение заключается в том, что переводит поперечную силу ( ), определенную из закона Гука в поперечную силу (
), определенную из закона Гука в поперечную силу ( ), определенную из уравнения равновесия пластины.
), определенную из уравнения равновесия пластины.
Из (2.45) вытекает, что между функциями  и
и  существует зависимость вида:
существует зависимость вида:
 , (2.47)
, (2.47)
где  - параметр, учитывающий влияние поперечных сдвигов.
- параметр, учитывающий влияние поперечных сдвигов.
Внося (2.47) в (2.45), получим уравнение для определения параметра  :
:
 . (2.48)
. (2.48)
Вводя в рассмотрение параметр
 , (2.49)
, (2.49)
уравнение (2.48) представим в виде:
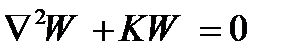 . (2.50)
. (2.50)
Разрешающее уравнение, полученное из (2.46), с учетом (2.47), имеет вид [9]:
 . (2.51)
. (2.51)
Внутренние усилия (2.44) представляются в форме классической теории пластин:
 (1.2)
(1.2)
 (2.52)
(2.52)

 (1.2)
(1.2)
Контурный интеграл (2.41) с учетом (2.47) запишется следующим образом:

 . (2.53)
. (2.53)
Значение параметра  , определенного из (2.49) имеет вид:
, определенного из (2.49) имеет вид:
 . (2.54)
. (2.54)
Отсюда видно, что параметр  , переводящий функцию прогибов
, переводящий функцию прогибов  в функцию
в функцию  (2.47) зависит от собственного числа уравнения (2.50)
(2.47) зависит от собственного числа уравнения (2.50)
Отметим, что уравнение (2.50) вытекает из равенства поперечных сил  и
и  , вычисленных по (2.52).
, вычисленных по (2.52).
Если потребовать, чтобы эти силы удовлетворяли уравнению равновесия пластины
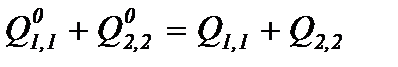 ,
,
то для определения параметра 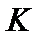 имеем уравнение четвертого порядка
имеем уравнение четвертого порядка
 . (2.55)
. (2.55)
Его аналогом является уравнение устойчивости пластины, сжатой в двух направлениях [15]:
 .
.
Считая, что пластина сжимается равномерно распределенной нагрузкой, т.е. полагая  , имеем:
, имеем:
 . (2.56)
. (2.56)
Сопоставляя уравнение (2.55) с уравнением (2.56) находим:
 . (2.57)
. (2.57)
Отсюда вытекает, что параметр 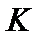 , входящий в формулу (2.54) является параметром нагрузки пластины, сжатой двух направлениях равномерно распределенной нагрузкой.
, входящий в формулу (2.54) является параметром нагрузки пластины, сжатой двух направлениях равномерно распределенной нагрузкой.
Уравнению (2.56) соответствует контурный интеграл (2.53) при  и с поперечной силой
и с поперечной силой
 . (2.58)
. (2.58)
Таким образом, для нахождения параметра 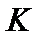 нет необходимости решать уравнение (2.55), а определить его можно с помощью аналогии установленной выше.
нет необходимости решать уравнение (2.55), а определить его можно с помощью аналогии установленной выше.
Достоинством данного варианта является то, что решение задачи изгиба с учетом поперечных сдвигов производится методами классической теории пластин, т.е. все решения, полученные ранее, можно использовать без особых трудностей с поправочным коэффициентом ( ) и тем самым установлена прямая связь теории пластин с учетом поперечных сдвигов с классической теорией.
) и тем самым установлена прямая связь теории пластин с учетом поперечных сдвигов с классической теорией.
Список литературы
1. Амбарцумян С.А. Теория анизотропных пластин. – 2-е изд., перераб. И доп. – М.: Наука, 1987. –360 с.
2. Власов Б.Ф. Об уравнениях теории изгиба пластин // Изв. АНСССР ОТН, 1957. - №12. – с.57-60.
3. Григолюк Э.И., Селезов И.Т. Неклассические теории колебаний стержней, пластин и оболочек // Итоги науки и техники. Механика твердого деформируемого тела. – М.: ВИНИТИ. 1973. – т.5. – 199с.
4. Григолюк Э.И., Чулков П.П. Устойчивость и колебания трехслойных оболочек. – М.: Машиностроение, 1973. –172с.
5. Королев В.И. Упругопластические деформации оболочек. – М.: Машиностроение, 1971. –304с.
6. Москаленко В.Н. К применению уточненных теорий изгиба пластинок в задаче о собственных колебаниях // Инженерный журнал. – М., 1961. – т.1. – вып.3. - с.93-101.
7. Пикуль В.В. Общая техническая теория тонких упругих пластин и пологих оболочек. –М.: Наука, 1977. – 151с.
8. Рябов О.Ф. Розрахунок багатошаро вих оболочек. – К.: Будвельник, 1968. –101с.
9. Турсунов К.А. Об одном варианте теорий изгиба трансверсально изотропных прямоугольных пластинок // Численные методы решения задач механики деформируемого твердого тела. – Караганда, 1987. – с. 92-97.
10. Уфлянд Я.С. Распространение волн при поперечных колебаниях стержней и пластин // Прикл.матем. и мех. – 1948. – т.12, - №3. – с. 287-300.
11. Bolle L. Contribution an probleme lineaire deflecsion dune plaque elastique // Bulletin technique de la Suisse Romande
- 1947. – 73/ - №21.281-285. - №22(1947). – 293-298.
12. Mindlin R.D. Influence of rotatory inertia and shear on flexural motions of isotropic elastic plates// J. Appl. Mech.
- 1951. – V18. – p. 31-38.
13. Вольмир А.С. Устойчивость деформируемых систем. – М.: Наука, 1967. –984с.
Date: 2016-05-24; view: 741; Нарушение авторских прав