Об одном методе расчета изгибаемой пластины

Рассмотрим прямоугольную пластину в декартовой системе координат .

Расчетные формулы, основанные на классической теории изгибаемой пластины [1], имеют вид:

ü внутренние усилия:

, ,

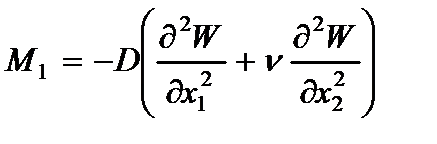, (2.59)

, ,

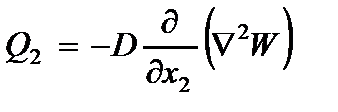где , 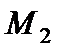- изгибающие моменты; 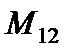- крутящий момент; , - поперечные силы; - цилиндрическая жесткость; 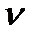- коэффициент Пуассона; 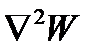- оператор Лапласа от функции прогибов ;

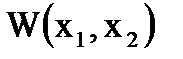ü уравнение равновесия пластины в усилиях:

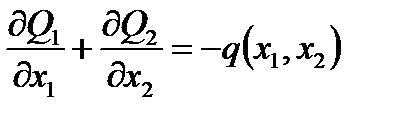, (2.60)

где 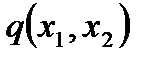- интенсивность внешней поперечной нагрузки;

ü разрешающее уравнение для определения функции прогибов пластины:

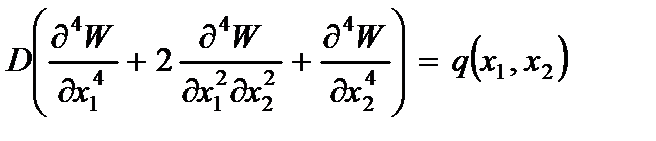. (2.61)

Решение уравнения (2.61) должно удовлетворять двум граничным условиям на каждом крае пластины. Для жестко закрепленного (защемленного), шарнирно опертого и свободного края 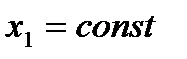, классическая теория пластины соответственно дает:

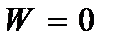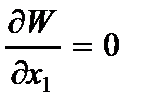, , (2.62)

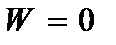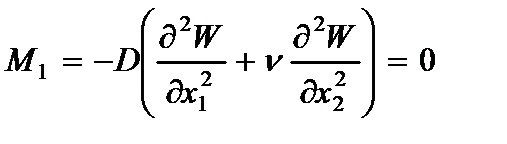, , (2.63)

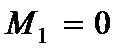, . (2.64)

Таким образом, чтобы произвести расчет пластины на изгиб, необходимо определить функцию прогибов 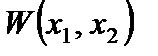из решения уравнения (2.61) с граничными условиями (2.62), (2.63) и (2.64).

Точные решения задачи изгиба пластины могут быть получены лишь в некоторых частных случаях, преимущественно для пластин постоянной толщины простой конфигурации и при определенных видах граничных условий (метод Навье, метод Леви). Применение прямых методов вариационного исчисления (метода Ритца, метода Бубнова-Галеркина и метода Канторовича-Власова) позволяет получить приближенные решения изгиба пластин при сложных граничных условиях.

Согласно методу Ритца функция прогибов отыскивается в виде ряда:

, (2.65)

где 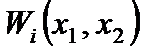- заданные координатные функции, каждая из которых удовлетворяет геометрическим граничным условиям; 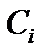- подлежащие определению коэффициенты из стационарности полной энергии пластины в виде системы линейных неоднородных алгебраических уравнений.

При применении метода Бубнова–Галеркина координатные функции выбираются так, что выполняются не только геометрические, но и статические граничные условия, а для определения неизвестных коэффициентов ряда (2.65) составляются следующие уравнения:

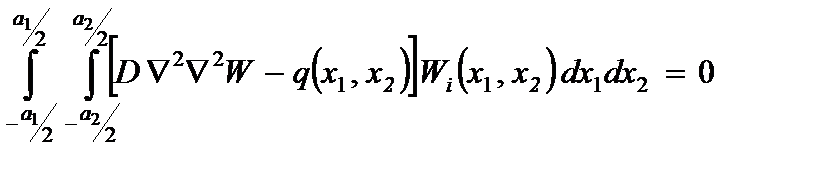, (2.66)

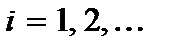
где в квадратной скобке под интегралом приведено уравнение (2.61).

В ряде случаев хорошие результаты можно получить с помощью метода Канторовича – Власова, позволяющего от уравнений в частных производных приближенно перейти к обыкновенным дифференциальным уравнениям. По этому методу функция прогибов задается в виде:

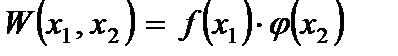, (2.67)

где - известная функция, удовлетворяющая геометрическим граничным условиям при ; 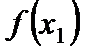- функция, подлежащая определению из уравнения, полученного из условия минимума полной энергии пластины

,

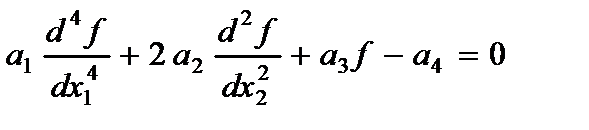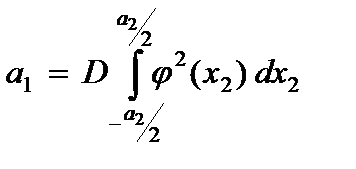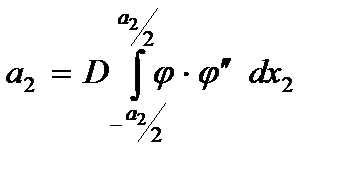, , (2.68)

, .

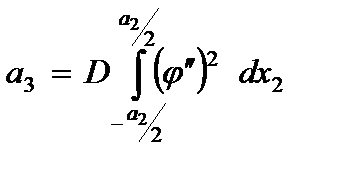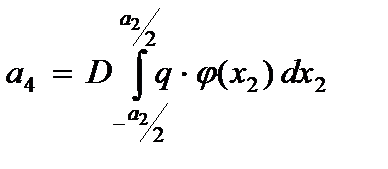Отметим, что при применении метода Ритца и Бубнова–Галеркина, чтобы получить удовлетворительные результаты, необходимо удерживать несколько членов ряда (2.65), а при применении метода Канторовича – Власова точность решения задачи зависит от выбора функции в выражении (2.67).

Изложенные выше методы в основном направлены на математическую сторону проблемы, а именно: при применении методов Ритца и Бубнова–Галеркина исходное уравнение в частных производных заменяется системой алгебраических уравнений n-ого (бесконечного) порядка; при применении же метода Канторовича – Власова оно заменяется дифференциальным уравнением четвертого порядка.

С точки зрения механики возникает проблема: изгиб пластины привести к изгибу балки. Предлагаемый метод, изложенный ниже, посвящен именно этой проблеме. Механический смысл этого метода заключается в том, чтобы заменить цилиндрическую жесткость рассчитываемой пластины обобщенной жесткостью заменяемой балки. С этой целью представим функцию прогибов в виде:

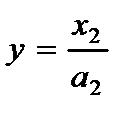, , (2.69)

где 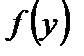- безразмерная функция, подлежащая определению; 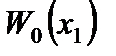- функция прогибов для балки.

Учитывая (2.69), запишем:

ü внутренние усилия (2.59):

,

,

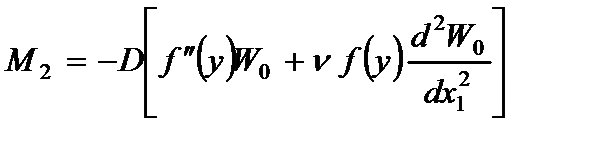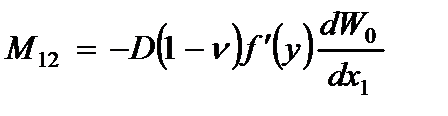, (2.70)

,

;

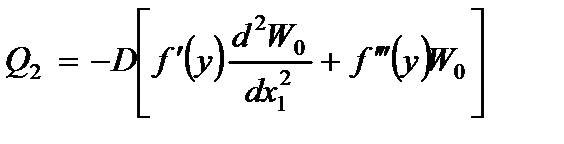ü разрешающее уравнение (2.61):

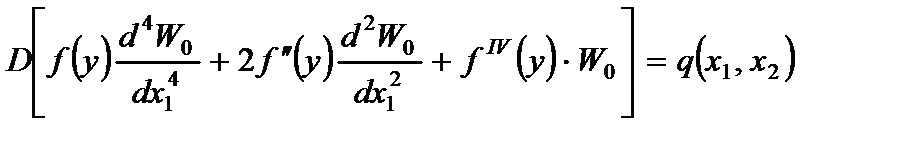. (2.71)

Введем интегральные характеристики для усилий и внешней нагрузки:

,

,

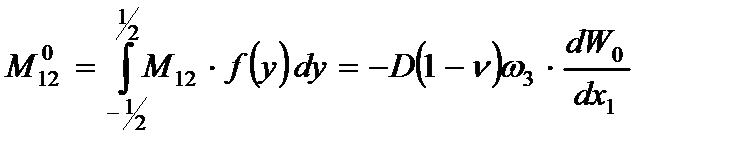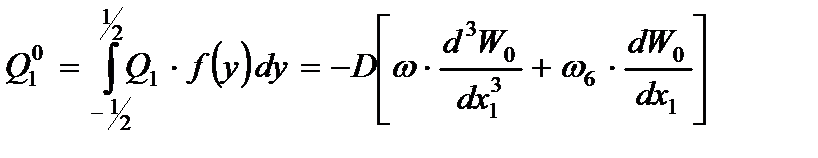, (2.72)

,

,

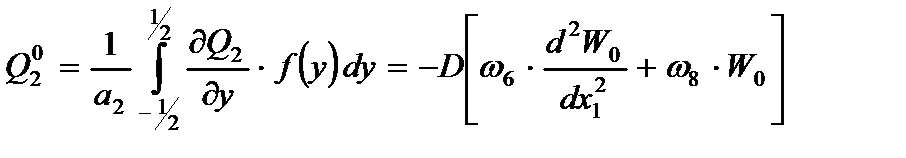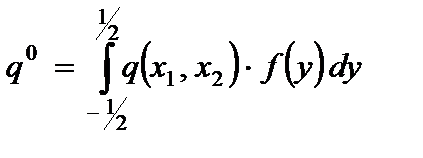где интегральные характеристики функции 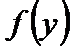вычисляются по следующим формулам:

, ,

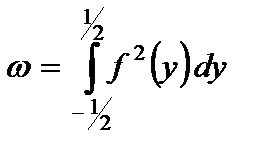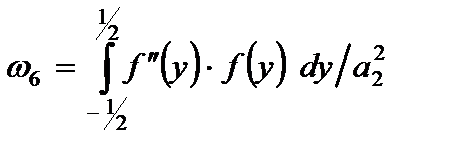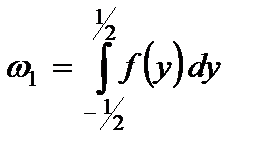, , (2.73)

.

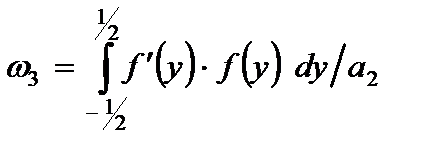Умножив (2.60) на 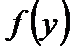и после интегрирования полученного выражения, с учетом (2.72) имеем уравнение равновесия в усилиях для обобщенной балки:

. (2.74)

Умножив (2.71) на 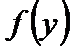и интегрируя полученное выражение в пределах от 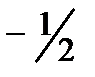до или подставляя в (2.74) значения усилий по (2.72), имеем разрешающее уравнение для определения балочной функции :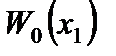

, (2.75)

которое по форме совпадает с уравнением метода Канторовича – Власова (2.68).

Учитывая уравнения переходных процессов, описывающих функцией :

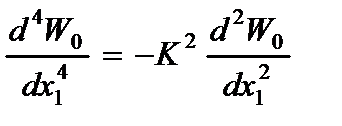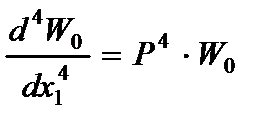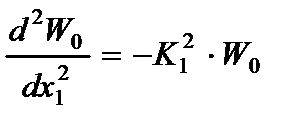, , , (2.76)

где 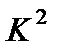, , 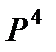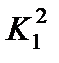- представляют собой собственные значения, представим (2.75) в форме уравнения изгиба обобщенной балки:

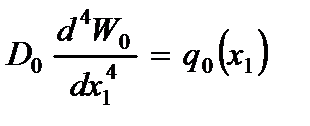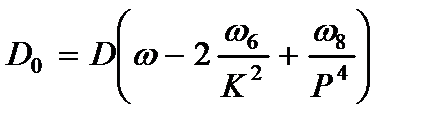, . (2.77)

Здесь 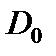- обобщенная жесткость балки, зависящая от собственных значени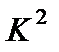й и .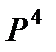

На основании (2.76) внутренние усилия балки (2.72) представляются следующим образом:

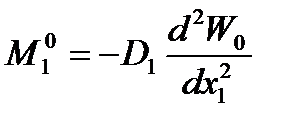, , (2.78)

, .

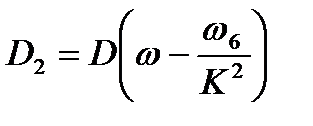Для определения жесткостных характеристик , , 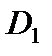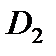поступаем следующим образом. Представим функцию прогибов обобщенной балки в виде:

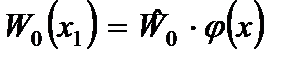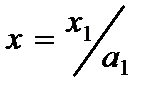, , (2.79)

где 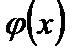- безразмерная функция прогибов; 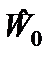- максимальный прогиб балки.

Учитывая (2.79), находим собственные значения уравнений (2.76):

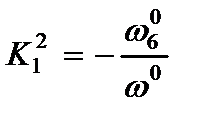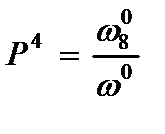, , , (2.80)

где параметры вычисляются по (2.73) с заменой на , на .

Обобщенные жесткости (2.77) и (2.78) с учетом (2.80) представляются следующим образом:

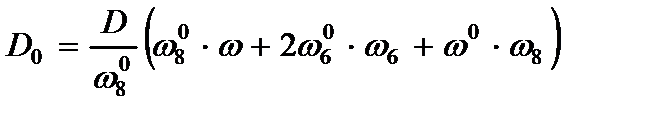, (2.81)

, .

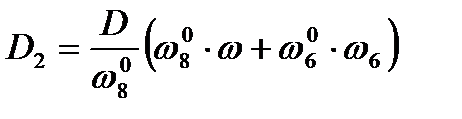Подставив (2.79) в (2.77) и умножив его на и после интегрирования, получим максимальный прогиб балки:

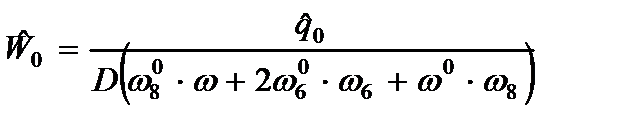, (2.82)

.

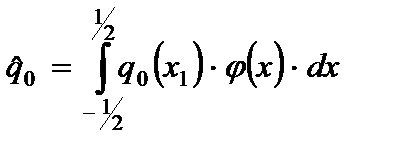Внося (2.79) в (2.77) и преобразуя его, получим разрешающее уравнение для функции :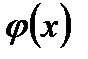

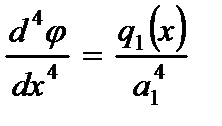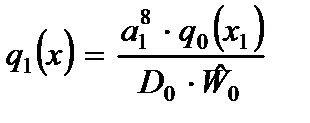, , , (2.83)

где 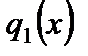- безразмерная интенсивность внешней нагрузки пластины 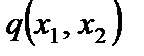по оси .

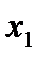Аналогичным образом, получим уравнение для определения функции :

, (2.84)

где 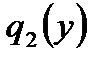- безразмерная интенсивность нагрузки пластины 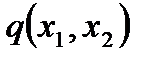по оси .

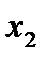Внося (2.79) в (2.78), имеем внутренние усилия, выраженные через функцию :

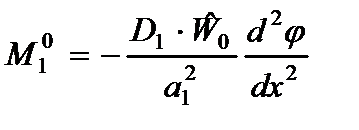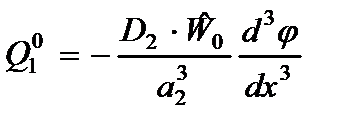, (2.85)

Произвольные постоянные, входящие в решение уравнения (2.83), находятся из следующих условий для края :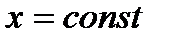

А) при шарнирном опирании концов:

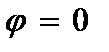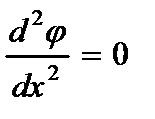, ; (2.86)

Б) при защемленных концах:

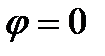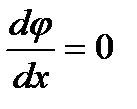, ; (2.87)

В) при свободных концах:

, . (2.88)

Для того чтобы сформулировать граничные условия для уравнения (2.84), запишем внутренние усилия пластины (2.59) на продольных сторонах с учетом (2.69), (2.79) и (2.80) в виде:

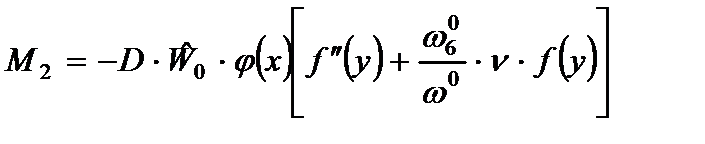, (2.89)

.

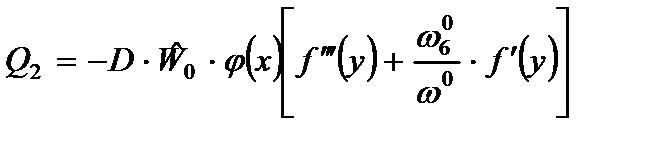Теперь произвольные постоянные, входящие в решение уравнения (2.84), можно определить из следующих условий для края :

А) при шарнирном опирании концов:

, или 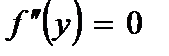, 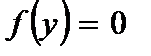; (2.90)

Б) при защемленных концах:

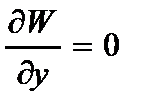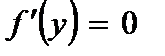, или , ; (2.91)

В) при свободных концах:

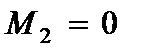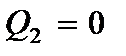, или ,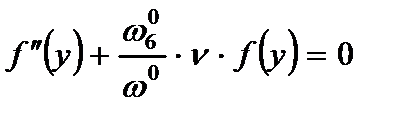

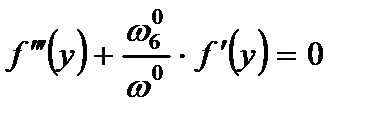. (2.92)

После расчета балки (определения функции 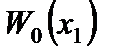) легко можно рассчитать пластину, представляя функцию прогибов в виде:

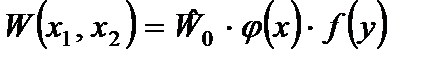. (2.93)

Порядок расчета пластины по предложенному методу рассмотрим на примере расчета квадратной пластины шарнирно опертой по контуру загруженной равномерно распределенной нагрузкой интенсивностью .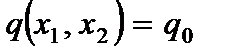

В этом случае безразмерные интенсивности нагрузки по условию расчета равны:

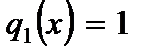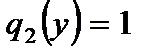, . (2.94)

Основные функции, являющиеся решениями уравнений (2.83) и (2.84), удовлетворяющие граничным условиям (2.86) и (2.90), имеют вид:

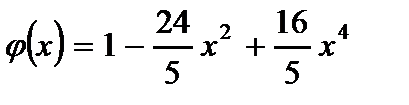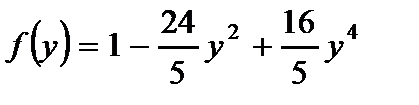, . (2.95)

Их интегральные характеристики согласно (2.73) принимают значения

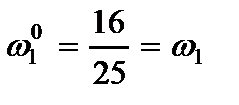, , (2.96)

, .

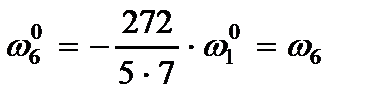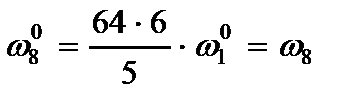Интенсивность внешней нагрузки согласно (2.82) равна:

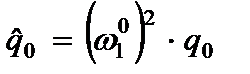. (2.97)

Внося (2.96) и (2.97) в (2.82), находим максимальный прогиб балки:

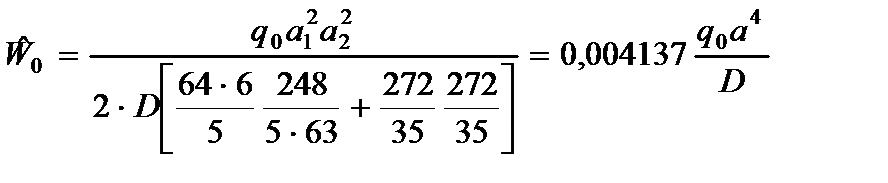. (2.98)

Данное решение полностью совпадает с решением, полученным методом разделения переменных [2].

Учитывая (2.98), по (2.79) находим функцию прогибов для балки и по (2.93) функцию прогибов для пластины.

Таким образом, предложенный метод по сравнению с другими аналитическими методами позволяет получить решение в простых полиномах и свести задачу изгиба пластины к задаче изгиба балки с обобщенной жесткостью, зависящей от формы изгиба. Сопоставление результатов расчета с имеющимися решениями указывает на правильность полученных формул.

Список литературы

1. Тимошенко С.П., Войновский–Кригер С. Пластинки и оболочки. Пер. с англ. Под ред. Г.С. Шапиро. М., Физматгиз, 1963. 635 с.

2. К.А.Д. Турсунов. Основы расчета прямоугольных пластин. – Караганда: КарГУ, 2001. – 72 с.

Date: 2016-05-24; view: 1167; Нарушение авторских прав