Напряжения в пластинке

Чтобы вычислить нормальные напряжения σ_x и σ_y воспользуемся двумя формулами закона Гука

(1.7)

и на основании третьей гипотезы отбросим напряжение σ_z. Получим:

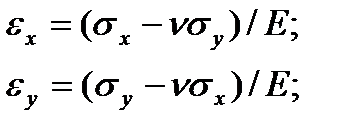
Отсюда, учитывая зависимости (1.6) найдем

(а)

Четвертая формула закона Гука после подстановки угловой деформации γ_xy из формул (1.6) принимает вид:

(б)

В двух других плоскостях касательные напряжения, согласно равенствам (1.1), обращаются в нуль:

Однако такой результат получен только вследствие принятых ранее гипотез. В действительности эти касательные напряжения не равны нулю, поскольку это противоречит условиям равновесия. Рассмотрим дифференциальные уравнения равновесия

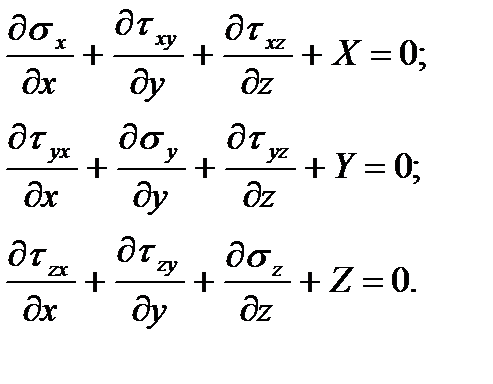(1.8)

Пренебрегая объемными силами, из первого уравнения найдем

Подставив сюда напряжения из формул (а) и (б) получим:

После упрощения получим

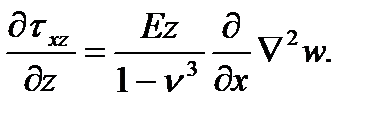
Проинтегрировав по z, найдем

(в)

Для определения произвольной функции f ₃ (x,y) имеем следующие граничные условия: на верхней и нижней поверхностях пластинки нет касательных нагрузок, т. е. при z =±h/2 τ_zx=0. Подставив эти условия в формулу (в), получим

откуда искомая функция

Вводя ее в формулу (в), получаем

(г)

Решив таким же путем второе уравнение равновесия (1.8), находим

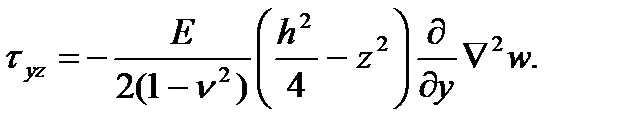(д)

Согласно формулам (а), (б), (г) и (д), в сечениях пластинки, перпендикулярных ее срединной плоскости, возникают следующие напряжения:

(1.9)

На рис. 1.2 показаны эпюры этих напряжений по толщине пластинки. Напряжения σ_x, σ_y и τ_xy = τ_yx распределяются по линейному закону, обращаясь в нуль в точках срединной плоскости; напряжения τ_zy и τ_zx распределяются по параболе, достигая в точках срединной плоскости максимального значения. Так же распределяются касательные напряжения и при поперечном изгибе балок прямоугольного сечения. В формулах (1.9) все напряжения выражены через одну функцию двух переменных w (x, y), следовательно, функция прогибов играет здесь ту же роль, что и функция напряжений в плоской задаче.

Рис. 1.2

Усилия в пластинке.

Найдем усилия, соответствующие напряжениям (1.9) в сечениях пластинки, нормальных к ее срединной плоскости. На рис. 1.3 изображен бесконечно малый элемент пластинки.

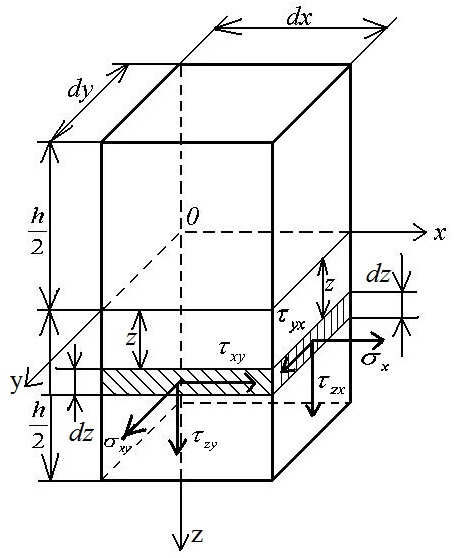
Рис. 1.3

На рисунке показаны положительные напряжения: нормальное напряжение σ _x направлено по внешней нормали к сечению, касательные – в направлении соответствующих положительных координатных осей.

Через N_x обозначим нормальную силу, приходящуюся на единицу ширины рассматриваемого сечения. Она равна проекции на ось x равнодействующей внутренних сил в сечении с нормалью, параллельной оси x. На ось x проецируется только нормальное напряжение σ _x. Соответствующая ему внутренняя сила на бесконечно малой площадке dydz равна σ _x dydz, а на единицу ширины сечения приходится сила σ _x dz. Суммируя эти элементарные силы по толщине пластинки, получим выражение нормальной силы

Подставим сюда нормальное напряжение σ _x из формул (1.9) и вынесем за знак интеграла величины, которые не зависят от координаты z:

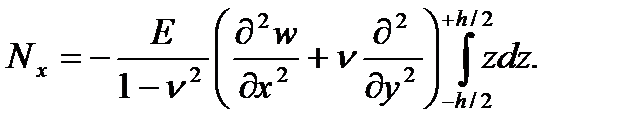
Под знаком интеграла стоит нечетная функция, а пределы интегрирования отличаются только знаком. Поэтому интеграл равен нулю, а нормальная сила N_x = 0.

Аналогичным способом определяется изгибающий момент M_x, представляющий собой сумму элементарных моментов

После интегрирования получим

Входящая сюда величина

(1.10)

называется цилиндрической жесткостью.

Поперечная сила в рассматриваемом сечении

Подставив в этот интеграл выражение касательного напряжения t_zx из формул (1.9) получим

Отсюда

Сдвигающую силу S_x находим, суммируя проекции внутренних сил в том же сечении на ось y:

После подстановки t_yx из формул (1.9)

S_x = 0.

Крутящий момент

(а)

Таким же способом определяются усилия в сечении с нормалью, параллельной оси y (Рис. 1.3):

(б)

Сравнив формулы (а)и (б), заметим, что

M_yx = M_xy = H.

Отсюда следует, что под действием поперечной нагрузки в сечениях пластинки, перпендикулярных ее срединной плоскости, возникают следующие усилия:
изгибающие моменты

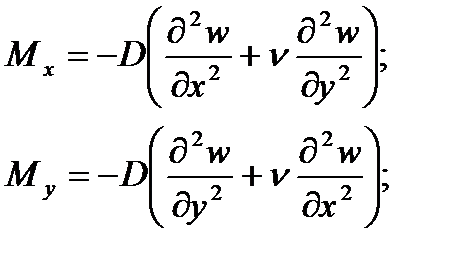(1.11)

поперечные силы

(1.12)

и крутящий момент

(1.13)

Все они выражены через прогибы срединной плоскости. Положительные направления указанных усилий показаны на рис. 1.4.

Рис. 1.4