
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Свойства преобразования Лапласа
|
|
- Абсолютная сходимость
Если интеграл Лапласа абсолютно сходится при  , то есть существует предел
, то есть существует предел
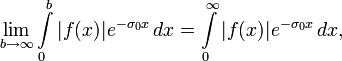
то он сходится абсолютно и равномерно для  и
и 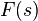 —аналитическая функция при
—аналитическая функция при  (
(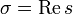 — вещественная часть комплексной переменной
— вещественная часть комплексной переменной  ). Точная нижняя грань
). Точная нижняя грань  множества чисел
множества чисел 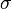 , при которых это условие выполняется, называется абсциссой абсолютной сходимости преобразования Лапласа для функции
, при которых это условие выполняется, называется абсциссой абсолютной сходимости преобразования Лапласа для функции  .
.
- Условия существования прямого преобразования Лапласа
Преобразование Лапласа 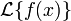 существует в смысле абсолютной сходимости в следующих случаях:
существует в смысле абсолютной сходимости в следующих случаях:
-
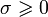 : преобразование Лапласа существует, если существует интеграл
: преобразование Лапласа существует, если существует интеграл 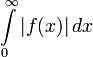 ;
; -
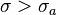 : преобразование Лапласа существует, если интеграл
: преобразование Лапласа существует, если интеграл 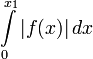 существует для каждого конечного
существует для каждого конечного  и
и 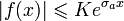 для
для 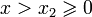 ;
; -
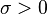 или
или 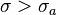 (какая из границ больше): преобразование Лапласа существует, если существует преобразование Лапласа для функции
(какая из границ больше): преобразование Лапласа существует, если существует преобразование Лапласа для функции  (производнаяот
(производнаяот  ) для
) для 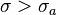 .
.
Примечание: это достаточные условия существования.
- Условия существования обратного преобразования Лапласа
Для существования обратного преобразования Лапласа достаточно выполнение следующих условий:
- Если изображение
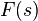 —аналитическая функция для
—аналитическая функция для 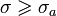 и имеет порядок меньше −1, то обратное преобразование для неё существует и непрерывно для всех значений аргумента, причём
и имеет порядок меньше −1, то обратное преобразование для неё существует и непрерывно для всех значений аргумента, причём 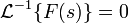 для
для  .
. - Пусть
 , так что
, так что 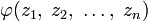 аналитична относительно каждого
аналитична относительно каждого 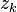 и равна нулю для
и равна нулю для  , и
, и 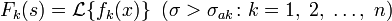 , тогда обратное преобразование существует и соответствующее прямое преобразование имеет абсциссу абсолютной сходимости.
, тогда обратное преобразование существует и соответствующее прямое преобразование имеет абсциссу абсолютной сходимости.
Примечание: это достаточные условия существования.
- Теорема о свёртке
Основная статья: Теорема о свёртке
Преобразованием Лапласа свёртки двух оригиналов является произведение изображений этих оригиналов:
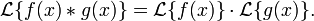
- Умножение изображений
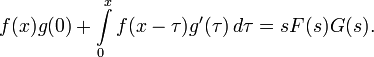
Левая часть этого выражения называется интегралом Дюамеля, играющим важную роль в теории динамических систем.
- Дифференцирование и интегрирование оригинала
Изображением по Лапласу первой производной от оригинала по аргументу является произведение изображения на аргумент последнего за вычетом оригинала в нуле справа:
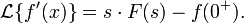
В более общем случае (производная  -го порядка):
-го порядка):

Изображением по Лапласу интеграла от оригинала по аргументу является изображение оригинала, делённое на свой аргумент:
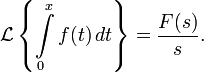
- Дифференцирование и интегрирование изображения
Обратное преобразование Лапласа от производной изображения по аргументу есть произведение оригинала на свой аргумент, взятое с обратным знаком:

Обратное преобразование Лапласа от интеграла изображения по аргументу есть оригинал этого изображения, делённый на свой аргумент:
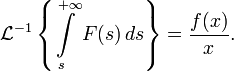
- Запаздывание оригиналов и изображений. Предельные теоремы
Запаздывание изображения:

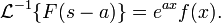
Запаздывание оригинала:


где 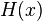 —функция Хевисайда.
—функция Хевисайда.
Теоремы о начальном и конечном значении (предельные теоремы):
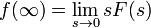 , если все полюсы функции
, если все полюсы функции  находятся в левой полуплоскости.
находятся в левой полуплоскости.
Теорема о конечном значении очень полезна, так как описывает поведение оригинала на бесконечности с помощью простого соотношения. Это, например, используется для анализа устойчивости траектории динамической системы.
- Другие свойства
Линейность:
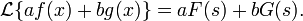
Умножение на число:

Date: 2016-05-23; view: 1017; Нарушение авторских прав