
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Понятие комплексного числа, действия над комплексными числами
|
|
Уже простейшие алгебраические операции над действительными числами (извлечение квадратного корня из отрицательного числа, решение квадратного уравнения с отрицательным дискриминантом) выводят за пределы множества действительных чисел. Дальнейшее обобщение понятия числа приводит к комплексным числам. Замечательным свойством множества комплексных чисел является его замкнутость относительно основных математических операций. Иначе говоря, основные математические операции над комплексными числами не выводят из множества комплексных чисел.
Комплексным числом  (в алгебраической форме) называется выражение
(в алгебраической форме) называется выражение

где  – произвольные действительные числа,
– произвольные действительные числа,  – мнимая единица, определяемая условием
– мнимая единица, определяемая условием  .
.
Число  называется действительной частью комплексного числа
называется действительной частью комплексного числа  , обозначается
, обозначается  (от латинского «realis»), число
(от латинского «realis»), число  называется мнимой частью комплексного числа
называется мнимой частью комплексного числа  и обозначается
и обозначается  (от латинского «imaginarius»).
(от латинского «imaginarius»).
Два комплексных числа 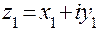 и
и  равны тогда и только тогда, когда равны их действительные и мнимые части:
равны тогда и только тогда, когда равны их действительные и мнимые части:  ,
,  . Два комплексных числа равны либо не равны (понятия «больше» и «меньше» для комплексных чисел не вводятся).
. Два комплексных числа равны либо не равны (понятия «больше» и «меньше» для комплексных чисел не вводятся).
Комплексно-сопряженным к числу  называется число
называется число  .Очевидно, комплексно–сопряженное число к числу
.Очевидно, комплексно–сопряженное число к числу  совпадает с числом
совпадает с числом  :
:  .
.
Арифметические операции. Сложение, вычитание и умножение комплексных чисел производят по обычным правилам алгебры.
Пусть 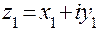 ,
,  . Тогда сумма
. Тогда сумма  , разность
, разность  , произведение
, произведение  , частное (при
, частное (при  )
)




Умножение и деление комплексных чисел в тригонометрической форме. Пусть числа  и
и  заданы в тригонометрической форме:
заданы в тригонометрической форме: 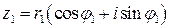 ,
, 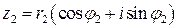 . Перемножим их:
. Перемножим их:
 .
.
Вспоминая формулы для косинуса и синуса суммы двух углов, получаем
 . (1)
. (1)
Мы видим, что при умножении комплексных чисел их модули перемножаются, а аргументы складываются. Геометрический смысл этой операции: представляя числа  и
и  векторами на комплексной плоскости, исходящими из нуль-точки, видим, что вектор
векторами на комплексной плоскости, исходящими из нуль-точки, видим, что вектор  получается из вектора
получается из вектора  «растяжением» в
«растяжением» в  раз и поворотом на угол
раз и поворотом на угол  .
.
Для частного получаем формулу:
 . (2)
. (2)
Возведение комплексного числа в степень. Из формулы (1) следует, что возведение в степень  комплексного числа
комплексного числа  производится по правилу
производится по правилу
 . (3)
. (3)
Извлечение корня из комплексного числа. Если комплексные числа  и
и  связаны соотношением
связаны соотношением  , то
, то  . Представим числа
. Представим числа  и
и  в тригонометрической форме:
в тригонометрической форме:
 ,
,  .
.
Будем считать, что здесь  – главное значение аргумента числа
– главное значение аргумента числа  .
.
Наша задача – по заданному числу  (т.е. по известным
(т.е. по известным 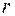 и
и  ) определить
) определить  (т.е.
(т.е.  и
и  ). В соответствии с формулой (3) равенство
). В соответствии с формулой (3) равенство  запишется в виде
запишется в виде
 .
.
Из равенства двух комплексных чисел в тригонометрической форме следует:
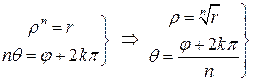 .
.
Здесь  – корень
– корень  - ой степени из действительного неотрицательного числа. Значит, для корня
- ой степени из действительного неотрицательного числа. Значит, для корня  -ой степени из комплексного числа
-ой степени из комплексного числа  получаем формулу
получаем формулу
 . (5)
. (5)
Полагая последовательно  , получим
, получим  различных значений
различных значений  :
:
 ,
,
 ,
,
…………………………………………………
 .
.
Все эти корни имеют одинаковые модули  , т.е. соответствующие точки располагаются на окружности радиуса
, т.е. соответствующие точки располагаются на окружности радиуса  с центром в начале координат. Аргументы двух соседних корней отличаются на угол
с центром в начале координат. Аргументы двух соседних корней отличаются на угол  . Значит, все значения корня
. Значит, все значения корня  -ой степени из комплексного числа
-ой степени из комплексного числа  находятся в вершинах правильного
находятся в вершинах правильного  -угольника, вписанного в окружность радиуса
-угольника, вписанного в окружность радиуса  .
.
Показательная форма комплексного числа. Формула Эйлера (будет доказана позже):
 , (6)
, (6)
позволяет записать комплексное число в показательной форме:
 , где
, где  .
.
Из формулы Эйлера и из  -периодичности синуса и косинуса следует:
-периодичности синуса и косинуса следует:

 .
.
Значит,  , т.е.
, т.е.  .
.
Date: 2016-05-23; view: 515; Нарушение авторских прав