Необходимые и достаточные условия существования экстремума функции одной и нескольких переменных

Сформулируем необходимые и достаточные условия существования условного экстремума.

Необходимые условия. Для того чтобы точка являлась точкой условного экстремума функции при уравнениях связи , необходимо, чтобы ее координаты при некоторых значениях 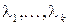удовлетворяли системе уравнений

Достаточные условия. Пусть функции

,

дважды непрерывно дифференцируемы в окрестности точки , а также пусть в этой точке выполняются необходимые условия существования условного экстремума функции при

.

Тогда если при выполнении условий

второй дифференциал функции Лагранжа является положительно (отрицательно) определенной квадратичной формой, то функция в точке имеет условный строгий минимум (максимум). Если второй дифференциал является неопределенной квадратичной формой, то в точке условного экстремума нет.

Если функция непрерывна на замкнутом ограниченном множестве 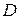, то она достигает на нем наибольшего и наименьшего значений. Эти значения она может принимать как во внутренних точках множества 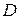(точки экстремума), так и на его границе. Следовательно, необходимо специальное исследование граничных точек множества.

Date: 2016-05-23; view: 501; Нарушение авторских прав