Методы одномерной оптимизации

Метод сканирования заключается в последовательном переборе всех значений х на [a,b] с шагом ε и вычислении критерияоптимальности R в каждой точке. Точка, в которой R принимает максимальное значение, принимается за решение задачи оптимизации.

На практике можно реализовать одну из основных модификаций метода – последовательное уточнение решения. На первом этапе сканирование осуществляют с крупным шагом. Затем отрезок, внутри которого получено наибольшее значение R, разбивается на более мелкие отрезки для нахождения уточненного значения экстремума.

Главный недостаток метода – возможность пропуска «острого» глобального максимума.

Метод дихотомии (половинного деления) заключается в делении заданного отрезка на две равные части с последующим выбором одной из них, в которой локализуется экстремум. Выбор отрезка осуществляется путем сравнения двух значений критерия оптимальности в точках, отстоящих от середины отрезка на ε/2.

Пусть х – середина [a,b]. Если R(x+ ε/2)=R(x- ε/2), то максимум достигается в точке х. Если R(x+ ε/2)>R(x- ε/2), то максимум располагается на правой половине текущего отрезка и для дальнейшего поиска выбирается отрезок [x- ε/2, b], в противном случае –
[a, x+ ε/2].

Процесс поиска завершается при достижении отрезком, на котором находится экстремум, величины ε.

Метод золотого сечения основан на делении текущего отрезка [a,b]на неравные части, подчиняющиеся правилу золотого сечения, с последующим выбором отрезка, содержащего экстремум.

Золотое сечение определяется по правилу: отношение всего отрезка к большей части равно отношению большей части к меньшей. Этому правилу удовлетворяют две точки c и d, расположенные симметрично относительно середины отрезка: . Если R(c)>R(d), то для поиска максимума выбирается [a,d], в противном случае – [c,b]. Процесс поиска завершается при достижении отрезком, на котором находится экстремум, величины ε.

В методе парабол предлагается аппроксимировать оптимизируемую функцию f(x) с помощью квадратичной функции

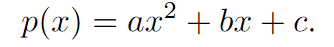
Пусть имеются три точки x1< x2< x3 такие, что интервал[x1, x3]содержит точку минимума функции f. Тогда коэффициенты аппроксимирующей параболы a, b, c могут быть найдены путем решения системы линейных уравнений:

Минимум такой параболы равен

Если 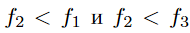, то точка u гарантированно попадает в интервал

Таким образом, внутри интервала определены две точки 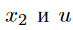, с помощью сравнения значений функции f в которых можно сократить интервал поиска В отличие от метода золотого сечения, метод парабол обладает суперлинейной скоростью сходимости. Однако, такая высокая скорость сходимости гарантируется только в малой окрестности точки минимума. На начальных стадиях процесса оптимизации метод парабол может делать очень маленькие шаг и или, наоборот, слишком большие шаги, приводящие к неустойчивым биениям.

Метод Фибоначчи является наиболее быстрым методом поиска, требующим минимального числа экспериментов. Здесь на каждом шаге, кроме первого, проводится не два, а один эксперимент. Стратегия поиска состоит в том, что новая точка поиска располагается внутри интервала неопределенности симметрично относительно уже находящейся там точки, оставшейся от предыдущих экспериментов. Для определения требуемого числа экспериментов, обеспечивающего точность, а также для выбора положения двух первых точек поиска, необходимо рассмотреть процесс поиска в обратном порядке, т.е. с последнего шага.

Рассмотрим ситуацию, которая возникла после того, как все эксперименты, кроме последнего, уже проведены. Длину изменяющегося интервала неопределенности обозначим 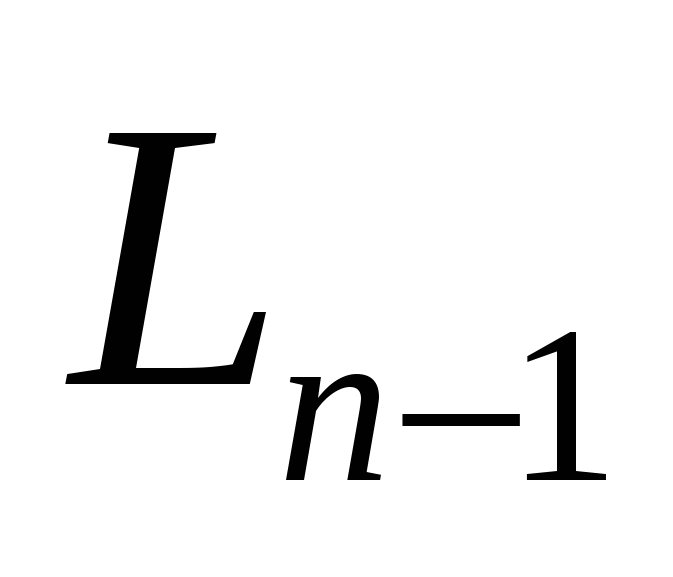. Внутри этого интервала находится эксперимент с наименьшим из 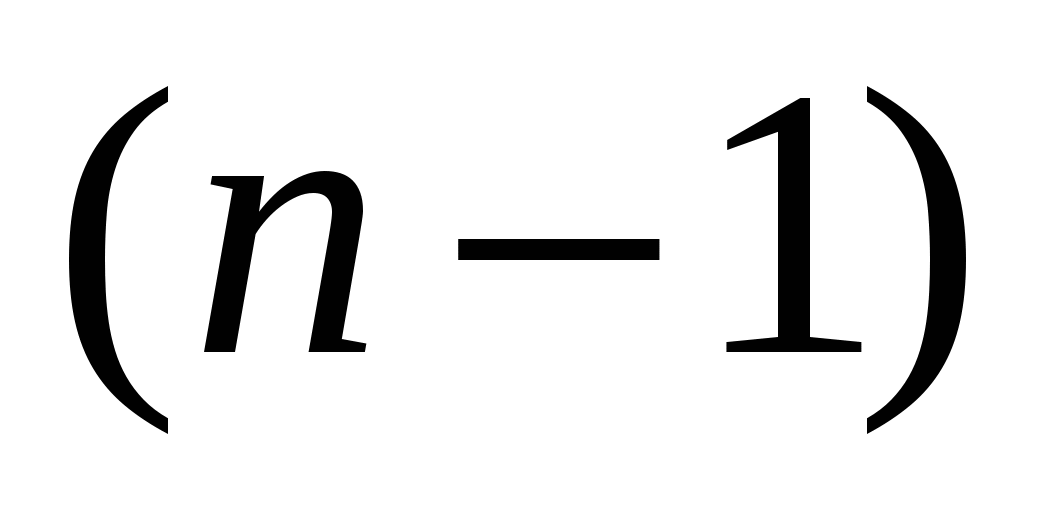испытаний значением функции и внутри него также следует провести последний эксперимент. Очевидно, что для обеспечения минимального интервала неопределенности 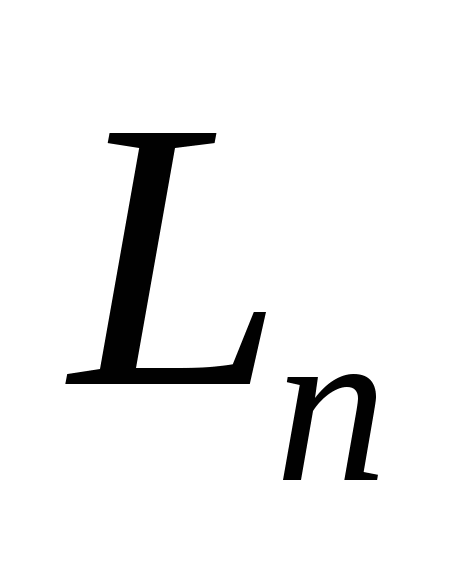после экспериментов указанные точки должны быть симметрично расположены относительно середины интервала и удалены от нее на расстояние .

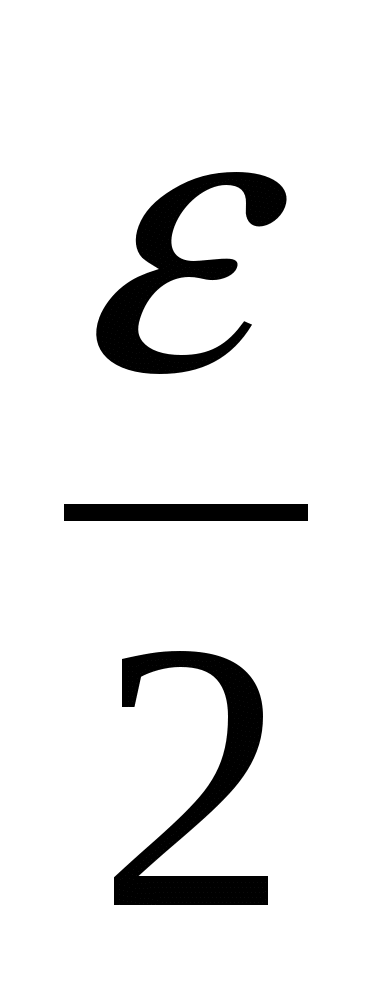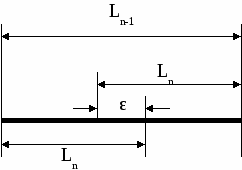
Словесный алгоритм метода следующий:

Заданы начало и конец интервала.

Шаг 1. Рассчитывается количество итераций и формируется массив чисел Фибоначчи.

Шаг 2. Рассчитываются две точк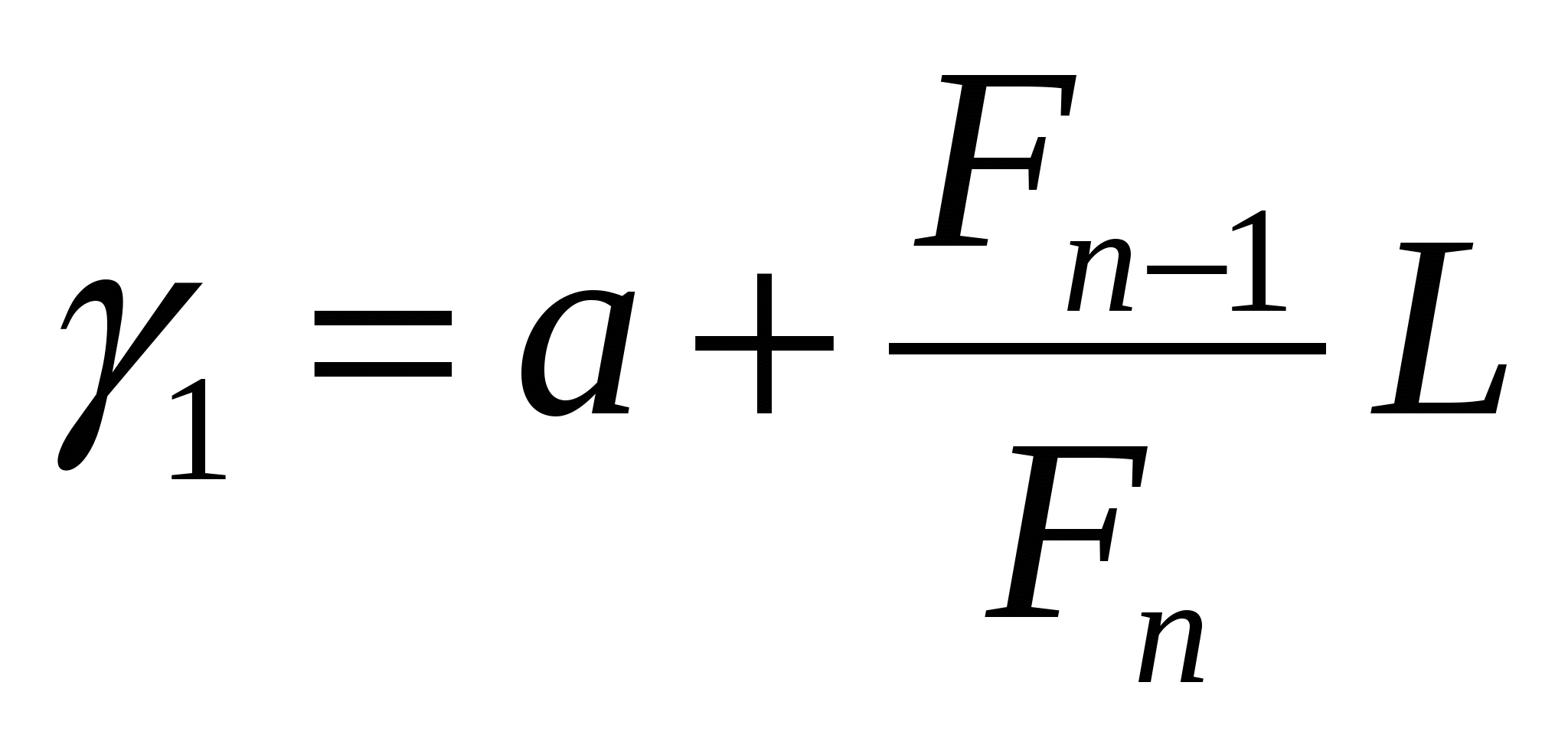и и 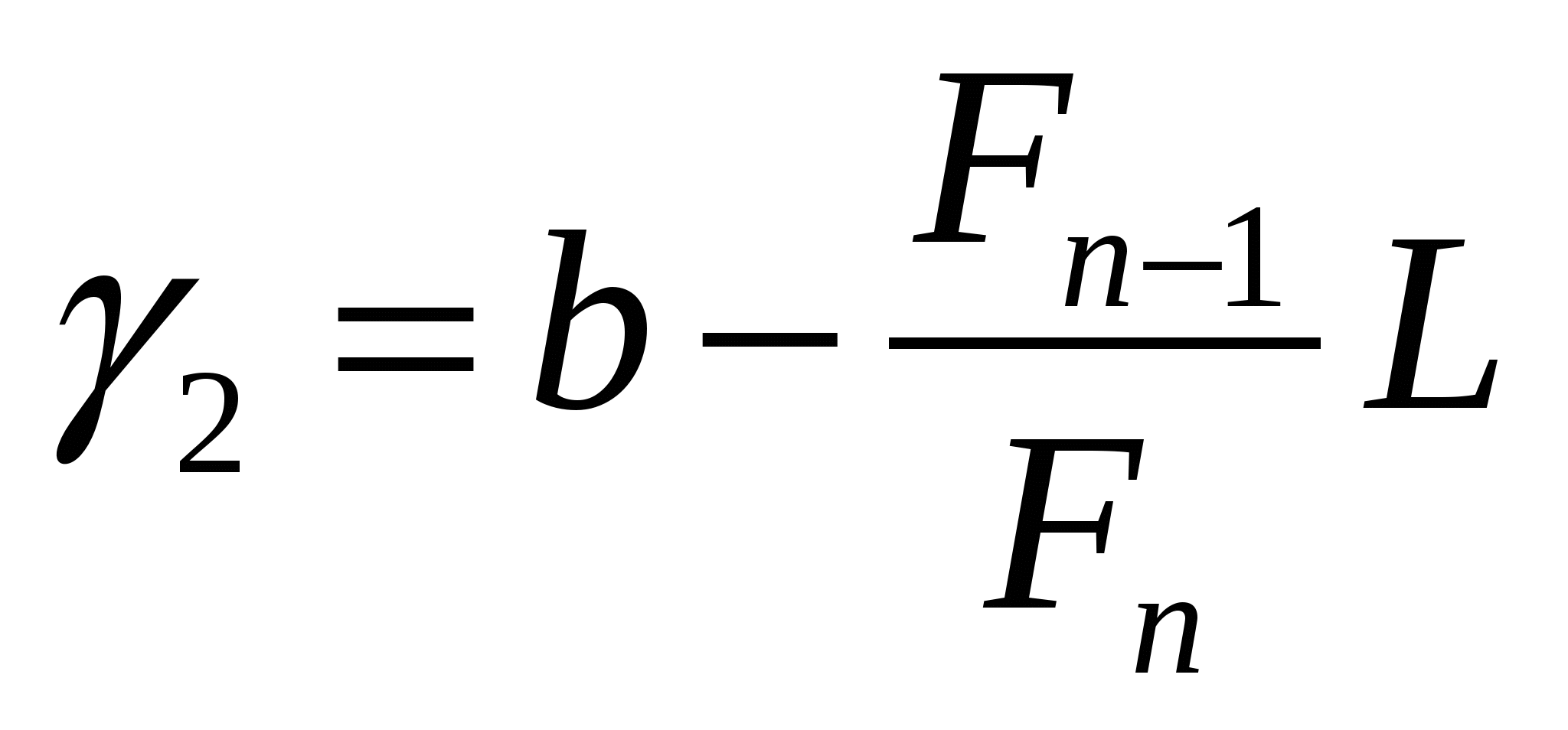и значения в них целевой функции и, где 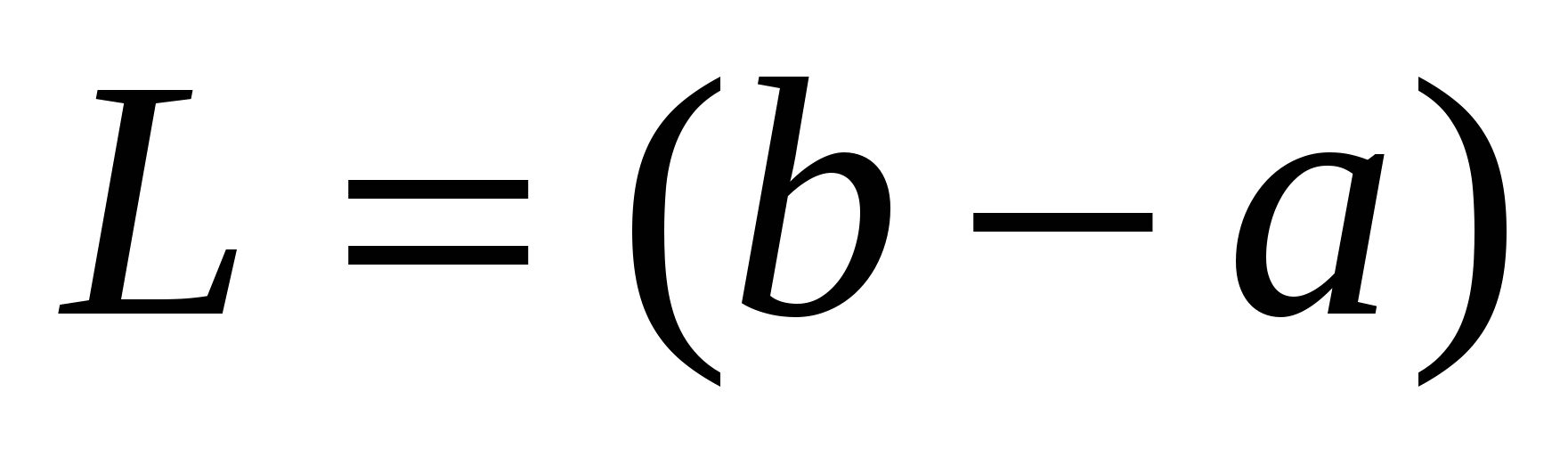– длина интервала.

Шаг 3. Если, то

, , ,

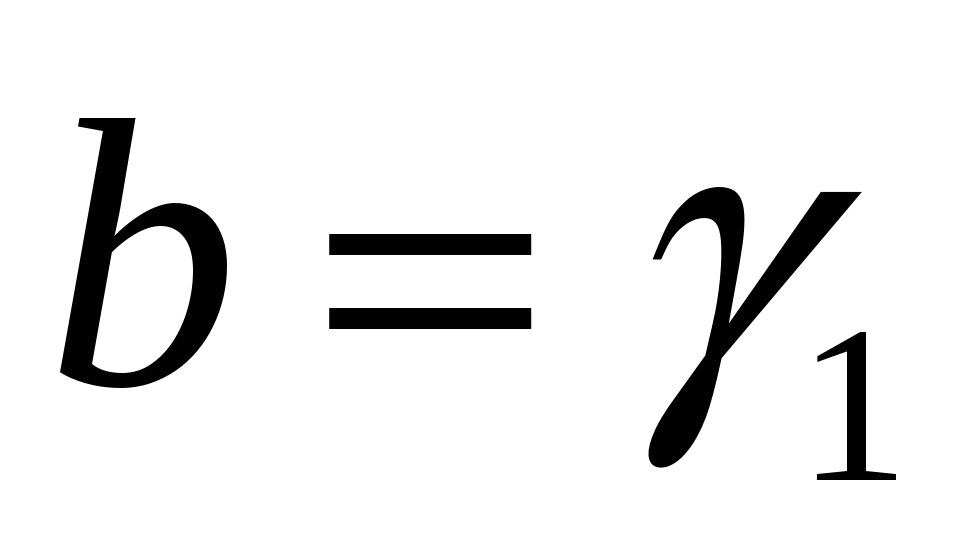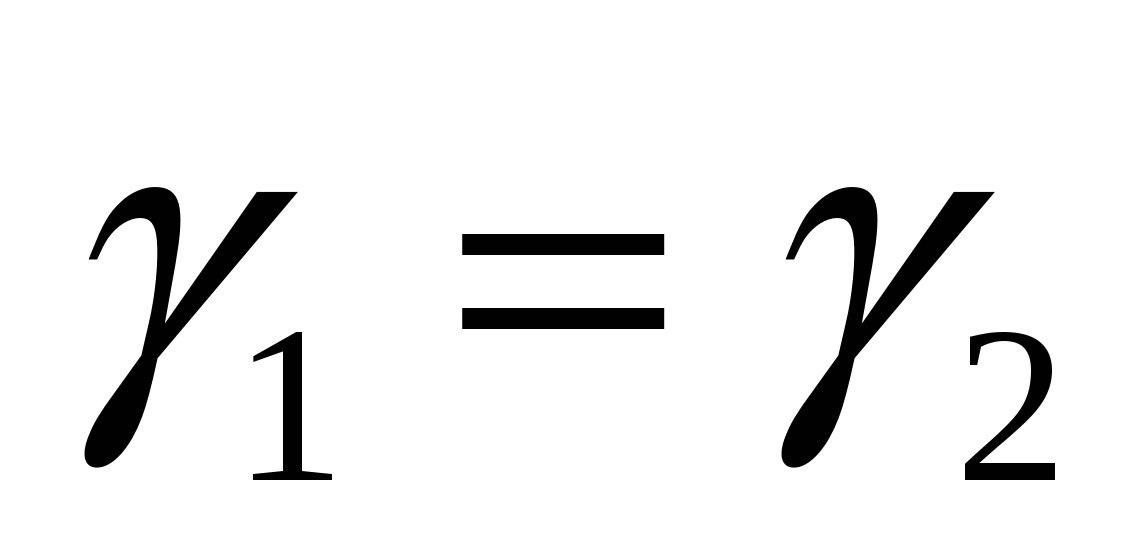и рассчитывается одна новая точка

,,

иначе

, , ,

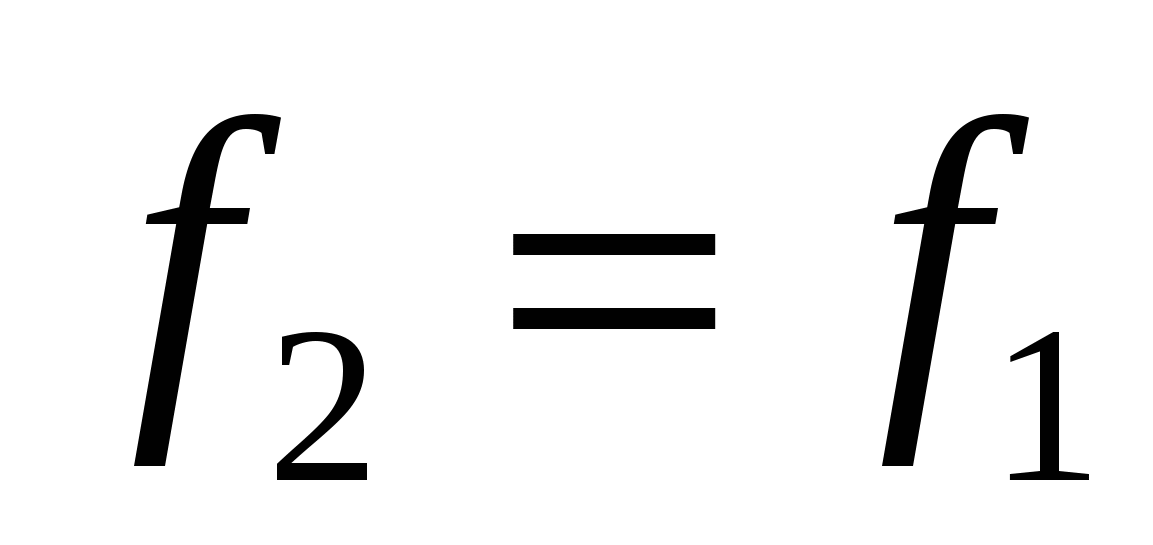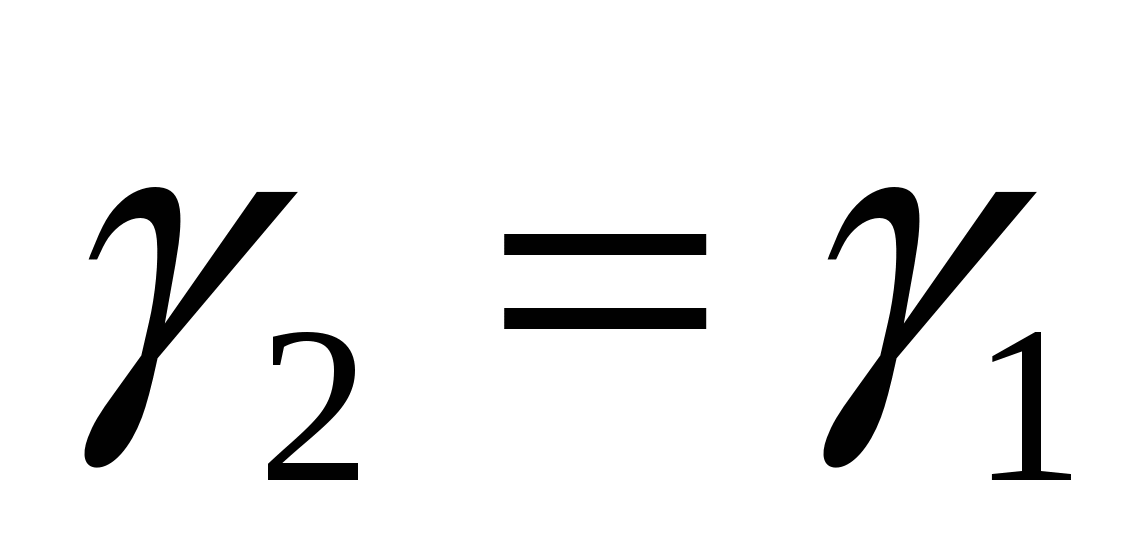и рассчитывается одна новая точка

,.

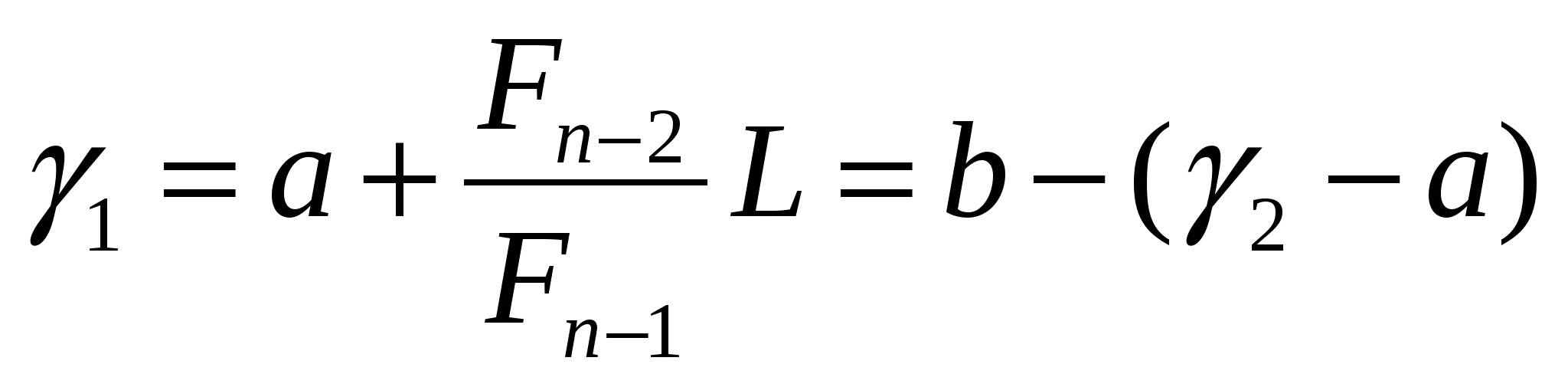Шаг 4. .

Шаг 5. Повторять шаги 1-3 до тех пор, пока .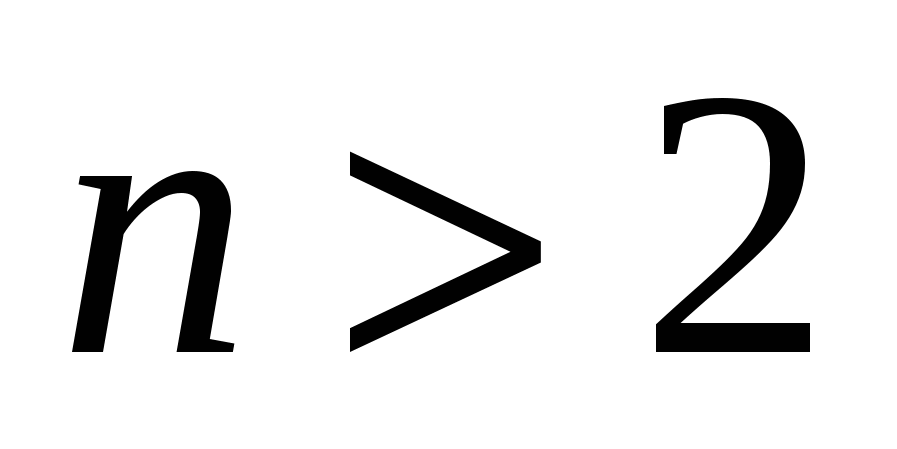

Шаг 6. Результат .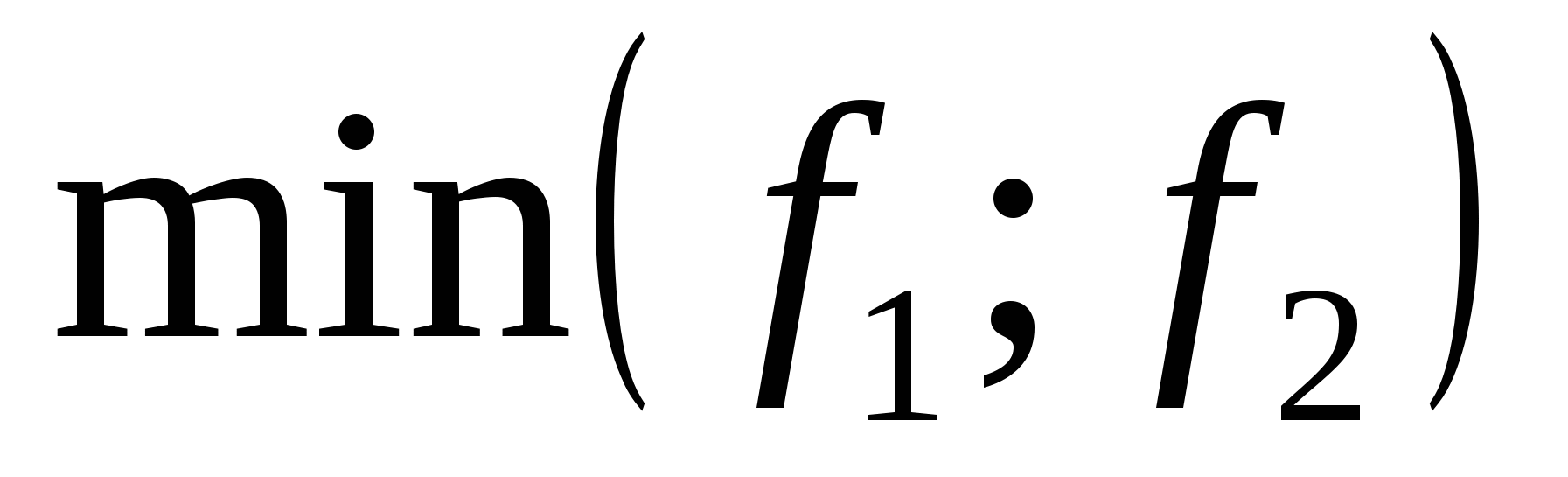

11. Градиентные методы многомерной оптимизации

Метод покоординатного спуска (градиента) формирует шаг по переменным как функцию от градиента R(x) в текущей точки последовательности. Градиент – это вектор из частных производных, который показывает направление и скорость возрастания функции.

Алгоритм поиска minR(x) в векторной форме записывается в виде: 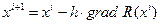, или в скалярном виде: 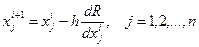, где h – величина рабочего шага, i – номер шага. Поиск максимума можно производить в обратном направлении градиента, т.е. 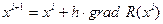или заменить на поиск минимума противоположной функции.

Выбор величины рабочего шага в направлении градиента зависит от величины градиента и сильно влияет на эффективность метода. Существует ряд алгоритмов коррекции величины h. Остановимся на выборе постоянного рабочего шага.

Для оценки частных производных можно применить алгоритм с парными пробами:

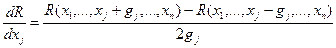, где g_j– пробный шаг по j-й переменной, выбираемый достаточно малым.

Условием окончания поиска может являться 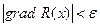, где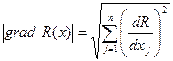

Основным недостатком метода является необходимость частого вычисления производных.

Метод наискорейшего спуска сочетает в себе метод градиента и методы одномерной оптимизации.

Алгоритм метода:

1. Выбирается начальная точка.

2. В текущей точке вычисляется градиент.

3. В направлении вычисленного градиента ищется 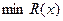любым методом одномерной оптимизации. Наиболее часто используется сканирование до первого локального минимума. Полученная точка локального минимума считается следующей точкой последовательности.

4. Повторяются пункты 2 и 3 до выполнения условия окончания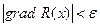

Можно использовать уменьшения рабочего шага после каждой смены направления, чтобы с большей точностью находить оптимум.

Date: 2016-05-23; view: 936; Нарушение авторских прав