Решение задачи оптимизации методом неопределенных множителей Лагранжа

Метод неопределенных множителей Лагранжа является классическим методом решения задач математического программирования. При практическом применении метода могут встретиться значительные вычислительные трудности, сужающие область его использования. Метод Лагранжа является аппаратом, используемым для обоснования различных современных численных методов. Рассмотрим задачу оптимизации max (min) z = ƒ(x); (6.3) φi(x) = bi (i = 1,...,m), x = (x1, x2,..., xn). (6.4) Эта задача выделяется из задачи (6.1), (6.2) тем, что среди ограничений (6.2) нет неравенств, нет условий не отрицательности переменных, их дискретности, m<n и функции ƒ(x) и φi(x) непрерывны и имеют частные производные, по крайней мере второго порядка. Последовательность решения данной задачи методом неопределенных множителей Лагранжа: 1) составить функцию Лагранжа L(x1,…, xn, λ1,…, λm) = ƒ(x1,..., xn) + 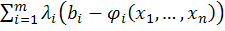; (6.5) λ1,…, λm – множители Лагранжа; 2) найти частные производные функции Лагранжа по всем переменным х1, х2,..., хп, λ1,…, λm (6.6) Получили систему уравнений(6.6), состоящую из n + m уравнений. Решить полученную систему (если это окажется возможным!) и найти таким образом все стационарные точки функции Лагранжа; 3) из стационарных точек, взятых без координат λ1,…, λm, выбрать точки, в которых функция ƒ(x) имеет условные локальные экстремумы при наличии ограничений (6.4). 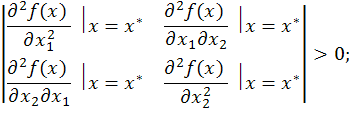Признаком существования минимума функции ƒ(x) в стационарнойточкех* является выполнение в ней достаточных условий минимума – выпуклости функции в окрестности этой точки, что может быть представлено следующим образом [*]: ⃒x= > 0; > 0, т.е. все определители должны быть положительны. Этот метод можно обобщить и на случай, когда переменные не отрицательны и некоторые ограничения заданы в форме неравенств.

Date: 2016-05-23; view: 649; Нарушение авторских прав