Нелокальные начальные и краевые задачи для уравнений с частными производными

Пусть дано некоторое уравнение в частных производных второго порядка в двух переменных (плоская задача). Суть метода сеток заключается в следующем:

1.Область интегрирования D, в которой требуется найти решение уравнения, покрывается сеткой, получающейся проведением параллельных осям координат прямых линий. Эти линии нужно провести таким образом, чтобы граница заданной области D лучше аппроксимировалась (приближалась) контуром сеточной области. Равномерную сетку можно построить следующим образом: сеточная область строится путем построения на плоскости двух семейств параллельных прямых:

, ,

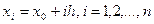где h -шаг сетки в направлении оси х, к – шаг сетки в направлении у. Точки пересечения этих прямых называются узлами. Два узла являются соседними, если они находятся друг от друга по направлениям х,у на расстоянии h или к. Обозначим через М множество узлов, принадлежащих области D с границей и узлов, лежащих вне D, но расположенных на расстоянии от границы D меньшем, чем h или к. Тогда узлы, у которых четыре соседних узлов принадлежат М, называются внутренними, например Р и Т. Узлы множества М, не являющиеся внутренними, являются граничными (узлы S, M, E, R).

2. Уравнение заменяется в узлах построенной сетки соответствующим конечно-разностным соотношением. В каждом внутреннем узле (Р,Т) заменим частные производные разностными отношениями. При подстановке разностных соотношений в ДУ заменяется системой линейных алгебраических уравнений. Решив систему, найдем значения искомой функции в узлах сетки, таким образом, получим численное решение заданного уравнения.

Замечание: Для граничных узлов, если эти узлы лежат на границе области, необходимо также использовать аппроксимирующие формулы. Если граничные узлы не лежат на границе, а на некотором расстоянии от нее, то необходимо провести интерполирование. Применение метода сеток покажем на примере уравнения теплопроводности.

Рассмотрим граничную задачу для уравнения теплопроводности, а именно найти функцию U, удовлетворяющую уравнению:

(1)

начальному условию

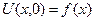, (2)

и краевым условиям

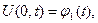
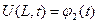(3)

Путем введения новой переменной 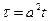уравнение приводится к виду:

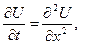
поэтому в дальнейшем примем а=1. Построим в полуполосе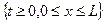

два семейства параллельных прямых 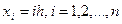; , обозначим и приближенно заменим в каждом внутреннем узле 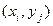производную разностным соотношением

, (4)

а производную 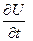одним из двух разностных соотношений

, (5)

(6)

Тогда для уравнения теплопроводности при а =1 получаем два типа конечноразностных уравнений:

, (7)

(8)

Обозначим и проводим эти уравнения к виду

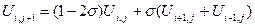, (9)

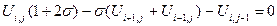(10)

Отметим, что для представления уравнения в сеточном виде была использована схема узлов, данная на рисунке 1 (а-явная схема, б-неявная схема).

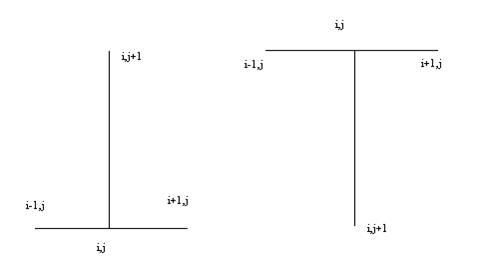
а-явная схема б-неявная схема

Рисунок 1. Схемы расположения узлов разностной сетки.

При выборе числа следует учитывать два обстоятельства:

1) погрешность замены ДУ разностным соотношением должна быть наименьшей;

2) разностное уравнение должно быть устойчивым.

Доказано, что уравнение (7) будет устойчивым при , а уравнение (8) – при любом . Наиболее удобный вид уравнение (7) имеет при :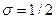

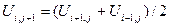
и при :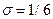

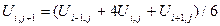
Контрольные вопросы:

1. Какому типу относятся уравнения диффузии и теплопроводности?

2. Как проводится дискретизация дифференциальных уравнений и области решения?

3. Метод определения устойчивости вычислительных конечно-разностных схем.

Лекция 5. Этапы компьютерного моделирования задач пищевой технологии. Примеры моделирования процессов пищевых технологий (тепловые процессы, экстракция, абсорбция, адсорбция)

План лекции:

1. Показать основные закономерности теплопередачи и их применение в пищевой инженерии.

2. Дифференциальные уравнения как основа модели диффузии и теплопередачи.

3. Реализация математической модели распространения температуры на одном примере.

Цель лекции: Разработка и реализация математической модели зависимости температуры от времени

Знания и умения, формируемые у магистранта: Формировать умение представлять физические закономерности распределения температуры в виде дифференциальных уравнений.

Форма проведения лекции: обзорная лекция

Математические модели используются в конечном счете для прогноза развития процессов во времени, состояния, в котором будет находиться объект, его свойств, если выполняются определенные условия. Для того, чтобы получить этот прогноз практически, недостаточно составить модель. Необходимо разработать и реализовать процедуру вычисления интересующих нас характеристик изучаемого процесса, идентифицировать модель, т.е. определить содержащие в ней так называемые внешние величины (коэффициенты, параметры, факторы), убедиться, что модель адекватна, т.е. дает практически приемлемые прогнозы. Необходимо, наконец, давать этот прогноз в тех случаях, когда это требуется. Термин «технология математического моделирования» будет использоваться для обозначения совокупности всех перечисленных действий, необходимых для практического получения прогноза течения процесса или прогноза свойств объектов, - от составления математической модели до вычисления прогнозируемых величин.

Date: 2016-05-23; view: 680; Нарушение авторских прав