Задача на охлаждение тел

Температура вынутого из печи хлеба в течение τ1 = 20 мин падает от t0 = 100 °C до t1 = 60 °C (рис. 4). Температура охлаждающего воздуха tс = 25 °C. Через какое время от момента начала охлаждения температура хлеба понизится до tк = 30 °С?

Здесь график

Зависимость среднеобъемной температуры тела при его охлаждении

от времени процесса

Решение.

Скорость охлаждения тела представляет собой понижение температуры тела t = t(τ) в единицу времени и выражается производной. По закону Ньютона скорость охлаждения тела пропорциональна разности температур тела и окружающей среды. Это процесс неравномерный. С изменением разности температур меняется и скорость охлаждения тела.

Дифференциальное уравнение охлаждения хлеба будет 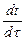= k (t – tc), (1)

где k – коэффициент пропорциональности, tc – температура среды.

Выражение (1) точнее следует называть не законом, а уравнением, формулой Ньютона, так как коэффициент k является сложной функцией многих переменных, он зависит от следующих факторов:

– скорости среды (жидкости, газа), обтекающей тело, ее плотности и вязкости, то есть переменных, определяющих режим течения жидкости;

– тепловых свойств жидкости (удельной теплоемкости, теплопроводности, коэффициента объемного расширения);

– тепловых свойств обтекаемого тела;

– геометрических параметров – формы и определяющих размеров, а также шероховатости поверхности тела.

Из этой сложной зависимости коэффициента пропорциональности k от многих параметров процесса следует, что простота уравнения (1) только кажущаяся. При его использовании трудности, связанные с определением количества тепла, передаваемого путем конвективного теплообмена, заключается в расчете величины k. В рассматриваемой задаче считаем коэффициент k постоянной величиной,которая должна быть задана непосредственно либо дополнительным

условием, из которого коэффициент k может быть определен. Уравнение (1) – обыкновенное дифференциальное уравнение первого порядка с разделяющимися переменными. Оно аналогично дифференциальному уравнению, описывающему бесконечное замедление тела, движущегося в среде с сопротивлением, пропорциональным скорости. Пусть τ – время охлаждения. Тогда, разделяя переменные, получим:

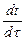= k dτ. (2)

Интегрируя уравнение (2),

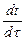= k, (3)

получаем:

t= k τ +, (4)

где A – произвольная положительная постоянная.

Из (4) следует общее решение уравнения (2):

t – tс =. (5)

Постоянную A определяем из начального условия t(0) = t0:

A = t0 – tс. (6)

Коэффициент пропорциональности k определяем из данного в

задаче дополнительного условия:

при τ = τ1 t(τ1) = t1.

Получаем:

t1 – tс = (t0 – tс). (7)

Таким образом, получили зависимость температуры тела от заданных начальной его температуры и температуры окружающей среды, а также от длительности процесса охлаждения. Необходимо отметить, что в данном случае можно определить только усредненную по объему температуру тела, но невозможно найти, например, температуру в центре тела либо в какой-нибудь другой его точке.

Из закона изменения температуры находим искомое время τк, необходимое для охлаждения хлеба от начальной его температуры t0 до конечной tк:

τк = τ1 мин. Замечание: если считать охлаждение тела происходящим по линейному закону (прямая АВ на рис. 4), получим искомое время охлаждения, равное 35 минутам, что, очевидно, ошибочно и недопустимо.

Контрольные вопросы:

1. Почему коэффициент пропорциональности не может быть представлен аналитической функцией?

2. Каков физический смысл начального условия для температуры и как его находить?

3. Какие методы существуют для установления адекватности результатов моделирования?

Лекция 6. Методы реализации математических моделей с применением компьютера. Понятие вычислительного эксперимента.

План лекции:

1. Какие методы существуют для реализации математических моделей на компьютере?

2. Рассмотрение аналитических методов реализации математических моделей.

3. Рассмотрение численных методов реализации математических моделей.

Цель лекции: Формирование у магистрантов понятия адекватности результатов расчетов по математическим моделям.

Знания и умения, формируемые у магистранта: умение проводить вычислительный эксперимент и устанавливать адекватность численных результатов

Форма проведения лекции: обзорная лекция

Задача 1.

Рассмотрим задачу нахождения простейшего закона нагрева теплообменника при постоянном притоке теплоты.

Решение.

Пусть Т – температура наружной поверхности теплообменника;

dT – изменение температуры отопительного аппарата в течение времени dt;

m – масса аппарата;

с – удельная теплоемкость материала аппарата;

α – коэффициент теплоотдачи (теплообмена) от поверхности аппарата;

Q – количество теплоты, поступающей в теплообменник в единицу времени;

S – поверхность теплообмена (теплоотдачи) аппарата;

Т 1 – наружная температура (температура среды);

Т – Т 1 – превышение наружной температуры теплообменника над температурой среды.

Требуется найти закон Т (t).

В течение времени dt происходят следующие процессы:

а) в теплообменник поступает количество теплоты, равное Qdt;

б) количество теплоты в аппарате изменяется на величину, равную mcdТ;

в) отдается в окружающую среду количество теплоты, равное величине α S (T – T 1) dt.

Суммируя эти количества, получаем уравнение теплового баланса (применение закона сохранения энергии к тепловым процессам):

mcdТ + α S (T – T 1) dt = Qdt, (1)

или

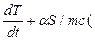T – T 1) = Q/mc. (2)

Полагая а = α S /(mc) и b = Q /(mc), получаем дифференциальное уравнение процесса (2) в следующем виде:

+ a (T – T 1) = b. (3)

Разделяем переменные, преобразуя при этом левую часть уравнения (3) так, чтобы в числителе получился дифференциал знаменателя:

- = dt. (4)

Интегрируя (4), получаем:

ln[ b- a (T- T 1)] -ln C 1=- at, (5)

где _С1 = соnst> 0, откуда следует

T – T 1 = + C ,

где С = – .

Используя начальное условие Т = Т₁ при t = 0, получаем

С = – b / а.

Тогда уравнение процесса примет вид:

T – T 1 = (1 – ), (6)

или, подставляя значения а и b, имеем:

T = T 1 + (1 – ). (7)

Рассмотрим этот закон ((7) или (6)).

При 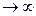T T T₁ + b / а = Т_k, где Т_k – конечная температура теплообменника.

Уравнение (6) может быть записано в виде

T (t) = Т_k – . (8)

Если Т₁ = 0, то Т_k = b / а и (8) будет

T = T_k (1 –– ). (9)

Подставляя в уравнение (9) значение t = 1/ а = τ, которое называется постоянной времени, получим:

T = T_k (1 – ) = 0,63 T_k. (10)

Задача 2.

В культуре пивных дрожжей быстрота прироста действующего фермента пропорциональна начальной его массе. Первоначальная масса фермента а в течение часа удвоилась. Во сколько раз она увеличится через 3 часа?

Решение.

По условию задачи дифференциальное уравнение процесса

= k x, (1)

где t – время, k – коэффициент пропорциональности.

(1) – уравнение с разделяющимися переменными, его общее решение

x = C , (2)

где С = const> 0.

Из начального условия (при t = 0 = a) имеем C = а. Поэтому частное решение имеет вид

x = a . (3)

Коэффициент k определяется из дополнительного условия:

при t = 1ч x= 2 а.

При этих условиях из (3) следует k =

Таким образом, окончательно получаем закон, которому подчиняется данный процесс, в виде

x = a2 , (4)

где τ = .

Из (4) получаем требование задачи: при t = 3ч x= 8 а, т. е. спустя 3 часа от начала процесса масса фермента увеличится в 8 раз.

Задача 3 для самостоятельного решения. Пусть при постоянной температуре скорость растворения твердого тела в жидкости пропорциональна массе этого вещества, еще могущего раствориться до полного насыщения жидкости. Найти закон зависимости массы

растворившегося вещества от времени.

Ответ: = P (1 – ),

где – масса растворившегося вещества; Р – масса вещества, дающая насыщенный раствор; t – время; k – эмпирический коэффициент пропорциональности.

Контрольные вопросы:

1. Как можно находить коэффициент пропорциональности из начальных условий?

2. Какие законы физики использованы при выводе уравнения для температуры?

3. Как можно найти ошибки моделирования, если имеются экспериментальные данные по процессу?

Date: 2016-05-23; view: 5402; Нарушение авторских прав