Методические рекомендации к лабораторному занятию. 1. Координата центра распределения определяет положение случайной величины на числовой оси и может быть найдена несколькими способами

1. Координата центра распределения определяет положение случайной величины на числовой оси и может быть найдена несколькими способами. Наиболее распространенным является отыскание центра по принципу симметрии, т. е. такой точки X_М на оси x, слева и справа от которой вероятности появления различных значений случайной величины одинаковы и равны 0,5.

При этом точку X_М называют медианой или 50 %-ной квантилью. Для его нахождения у распределения случайной величины должен существовать только нулевой начальный момент. Нулевым моментом в математической статистике называют некоторое среднее значение, отсчитываемое от начала координат. Нулевой начальный момент равен единице.

Первым начальным моментом, как известно, является математическое ожидание случайной величины. В качестве оценки центра распределения может выбираться одна из следующих оценок (в зависимости от типа распределения): выборочное среднее арифметическое, медиана, центр размаха, срединный размах. При выборе оценок центра распределения следует учитывать, что они имеют различную чувствительность к наличию промахов в обрабатываемой совокупности исходных данных.

2. Определить оценки центра распределениярезультатов наблюдений при многократных измерениях по следующим формулам:

- среднее арифметическое (формула 3.3.2);

- среднее арифметическое 90 %-ной выборки:

, (3.5.1)

где 2 r – число не учитываемых результатов;

- медиана распределения:

; (3.5.2)

- срединный размах:

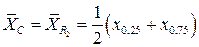, (3.5.3)

где , – 25 % и 75 %-ные квантили опытного распределения, которые представляют собой усредненные значения конкретных результатов наблюдений. Например, для выборки 50 штук этими квантилями являются точки между 12 и 13, а также между 38 и 39 результатами;

- центр размаха:

, (3.5.4)

где 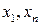– крайние значения вариационного ряда.

2. Расположить полученные оценки центра распределения в вариационный ряд: . За оценку центра распределения принимается оценка, которая занимает медианное положение в ряду.

3. Определить оценку средней квадратичной погрешности результатов наблюдений по формуле:

. (3.5.5)

4. Определить оценку средней квадратичной погрешности результата измерения по формуле:

. (3.5.6)

Полученные результаты занести в таблицу 3.5.1.

Таблица 3.5.1 – Отчет лабораторной работы

xi
mi

Рассмотрим на примере последовательность определения оценок центра распределения.

Получены результаты 20 измерений сопротивления резисторов. Результаты измерений по возрастанию и частота их появления указаны в таблице 3.5.2.

Таблица 3.5.2 – Результаты наблюдений

Требуется определить оценки результата измерения и СКО результатов наблюдений и измерения.

Будем считать, что закон распределения не известен. В этом случае за оценку центра распределения экспериментальных данных принимают медиану из ряда пяти оценок центров (расположенных в вариационный ряд).

Определяем оценку центра:

1. Среднее арифметическое по формуле 3.3.2:

Ом.

2. Среднее арифметическое 90 %-ной выборки определяем по формуле 3.5.1.

Пять процентов выборки в нашем случае , т. е. один результат измерения. Отбрасываем по одному измерению с концов вариационного ряда, т. е. результаты x₁ = 23,0 мкм и x₂₀ = 23,7 мкм. Тогда:

Ом.

3. Медиану распределения определяем с учетом, что n -четное, по формуле 3.5.2:

Ом.

4. Вычисляем 25 % и 75 %-ные квантили опытного распределения. Этими квантилями являются точки между 4 и 5, а также между 16 и 17 результатами:

Ом; Ом.

Тогда по формуле 3.5.3:

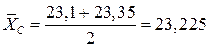Ом.

5. Центр размаха определяем по формуле 3.5.4:

Ом.

6. Полученные оценки центра распределения располагаем в вариационный ряд:

или 23,20<23,225<23,25<23,26<23,35 Ом. (5.5)

За оценку центра распределения (результата измерения) окончательно принимаем среднее арифметическое 90 %-ной выборки, так как эта оценка занимает медианное положение в ряду оценок: Ом.

7. Оценку средней квадратичной погрешности результатов наблюдений вычисляем по формуле 3.5.5:

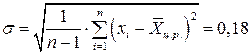Ом.

8. Оценку средней квадратичной погрешности результатов измерений определяем по формуле 3.5.6:

Ом.

Date: 2016-05-18; view: 428; Нарушение авторских прав