
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Методические рекомендации к лабораторному занятию. 1. Грубые погрешности (промахи) относятся к числу погрешностей, изменяющимся случайным образом при повторных наблюдениях
|
|
1. Грубые погрешности (промахи) относятся к числу погрешностей, изменяющимся случайным образом при повторных наблюдениях. Они явно превышают по своему значению погрешности, оправданные условиями проведения эксперимента. Под промахом понимается значение погрешности, отклонение которого от центра распределения существенно превышает значение, оправданное объективными условиями измерения. Поэтому с точки зрения теории вероятности появление промаха маловероятно.
2. Причинами грубых погрешностей могут быть неконтролируемые изменения условий измерений, неисправность, ошибки оператора и др. Для исключения грубых погрешностей применяют аппарат проверки статистических гипотез. В метрологии используются статистические гипотезы, под которыми понимают гипотезы о виде неизвестного распределения, или о параметрах известных распределений.
3. Исключение грубых погрешностей из результатов измерений проводится в следующей последовательности:
1. Для графического определения вида закона распределения построить гистограмму распределения результатов измерений по частоте.
2. Вычислить значения  и
и 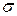 по формулам:
по формулам:
 ; (3.6.1)
; (3.6.1)
 , (3.6.2)
, (3.6.2)
где  коэффициент смещения.
коэффициент смещения.
Таблица 3.6.1 – Значения коэффициента Mk в зависимости от количества наблюдений n
| n | Mk | n | Mk | n | Mk |
| 1,253 | 1,025 | 1,013 | |||
| 1,128 | 1,023 | 1,012 | |||
| 1,085 | 1,021 | 1,010 | |||
| 1,064 | 1,019 | 1,008 | |||
| 1,051 | 1,018 | 1,007 | |||
| 1,042 | 1,017 | 1,006 | |||
| 1,036 | 1,016 | 1,006 | |||
| 1,032 | 1,015 | 1,005 | |||
| 1,028 | 1,014 | 1,004 |
3. Определить критерии, установленные для определения грубой погрешности подозрительного результата  при измерении:
при измерении:
- проверка по критерию "3 σ ".
Подозрительный результат не является грубой погрешностью, если выполняется условие:
 ; (3.6.3)
; (3.6.3)
- проверка по критерию Смирнова.
Из таблицы 3.6.2 для заданного уровня значимости и объема выборки находится значение βk. Наличие грубой погрешности не подтверждается, если выполняется условие:
 ; (3.6.4)
; (3.6.4)
Таблица 3.6.2 – Квантили распределения βk
Объем выборки 
| Предельное значение βk при уровне значимости q | ||||
| 0,100 | 0,050 | 0,0010 | 0,005 | 0,001 | |
| 1,282 | 1,645 | 2,326 | 2,576 | 3,090 | |
| 1,632 | 1,955 | 2,575 | 2,807 | 3,290 | |
| 1,818 | 2,121 | 2,712 | 2,935 | 3,403 | |
| 1,943 | 2,234 | 2,806 | 3,023 | 3,481 | |
| 2,036 | 2,319 | 2,877 | 3,090 | 3,540 | |
| 2,111 | 2,386 | 2,934 | 3,143 | 3,588 | |
| 2,172 | 2,442 | 2,981 | 3,188 | 3,628 | |
| 2,224 | 2,490 | 3,022 | 3,227 | 3,662 | |
| 2,269 | 2,531 | 3,057 | 3,260 | 3,692 | |
| 2,309 | 2,568 | 3,089 | 3,290 | 3,719 | |
| 2,559 | 2,799 | 3,289 | 3,480 | 3,890 | |
| 2,635 | 2,870 | 3,351 | 3,539 | 3,944 | |
| 2,696 | 2,928 | 3,402 | 3,587 | 3,988 | |
| 2,792 | 3,015 | 3,480 | 3,662 | 4,054 | |
| 2,860 | 3,082 | 3,541 | 3,716 | 4,108 | |
| 3,076 | 3,285 | 3,723 | 3,892 | 4,263 |
- проверка по критерию Романовского.
Определяем характеристики распределения без учета подозрительного результата:
 , (3.6.5)
, (3.6.5)
 . (3.6.6)
. (3.6.6)
По таблице 3.6.3 находим коэффициент Стьюдента при объеме выборки  и заданной доверительной вероятности.
и заданной доверительной вероятности.
Таблица 3.6.3 – Критерий Стьюдента  (квантили Стьюдента)
(квантили Стьюдента)
| Довери- тельная вероят- ность Р | Число степеней свободы k | |||||||||||||

| ||||||||||||||
| 0,90 | 2,35 | 2,13 | 2,01 | 1,94 | 1,86 | 1,81 | 1,78 | 1,73 | 1,72 | 1,70 | 1,68 | 1,67 | 1,66 | 1,64 |
| 0,95 | 3,18 | 2,78 | 2,57 | 2,45 | 2,31 | 2,23 | 2,18 | 2,10 | 2,07 | 2,04 | 2,02 | 2,00 | 1,98 | 1,96 |
| 0,99 | 5,84 | 4,60 | 4,03 | 3,71 | 3,36 | 3,17 | 3,06 | 2,98 | 2,82 | 2,75 | 2,70 | 2,86 | 2,62 | 2,58 |
Наличие грубой погрешности не подтверждается, если выполняется условие:
 . (3.6.7)
. (3.6.7)
- проверка по критерию Ирвина.
Для полученных экспериментальных данных определяют коэффициент по формуле:
 . (3.6.8)
. (3.6.8)
Затем этот коэффициент сравнивается с табличным значением  , значения которого приведены в таблице 3.6.4.
, значения которого приведены в таблице 3.6.4.
Таблица 3.6.4 – Критерий Ирвина 
| Число измерений n | Уровень значимости | |

| 
| |
| 2,8 | 3,7 | |
| 2,2 | 2,9 | |
| 1,5 | 2,0 | |
| 1,3 | 1,8 | |
| 1,2 | 1,7 | |
| 1,1 | 1,6 |
Нулевая гипотеза о грубой погрешности не подтверждается, если выполняется условие:
 . (3.6.9)
. (3.6.9)
- проверка по критериювариационного размаха.
Для его использования определяют размах вариационного ряда упорядоченной совокупности наблюдений  :
:
 . (3.6.10)
. (3.6.10)
Выполняем проверку по следующему неравенству:
 , (3.6.11)
, (3.6.11)
где  выборочное среднее арифметическое значение, вычисленное после исключения предполагаемого промаха;
выборочное среднее арифметическое значение, вычисленное после исключения предполагаемого промаха;
 критериальное значение (таблица 3.6.5).
критериальное значение (таблица 3.6.5).
Таблица 3.6.5 – Критерий вариационного размаха

| 8 –9 | 10 –11 | 12 – 15 | 16 – 22 | 23 – 25 | 26 – 63 | ||||

| 1,7 | 1,6 | 1,5 | 1,4 | 1,3 | 1,2 | 1,1 | 1,0 | 0,9 | |
- проверка по критерию Диксона.
При использовании критерия вычисляют коэффициент Диксона (наблюдаемое значение критерия) для проверки наибольшего или наименьшего экстремального значения в зависимости от числа измерений. В таблице 3.6.6 приведены формулы для вычисления коэффициентов.
Таблица 3.6.6 – Формулы коэффициентов Диксона
Объем выборки 
| Коэффициент Диксона | Для наименьшего экстремального значения параметра | Для наибольшего экспериментального параметра |
| 3 – 7 | 
| 
| 
|
| 8 – 10 | 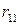
| 
| 
|
| 11 – 13 | 
| 
| 
|
| 14 – 25 | 
| 
| 
|
Таблица 3.6.7 – Критериальные значения коэффициентов Диксона (при принятом уровне значимости q)
| Коэффициент Диксона | Число измерений |  при уровне значимости при уровне значимости 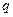
| |||
| 0,1 | 0,05 | 0,02 | 0,01 | ||

| 0,886 0,679 0,557 0,482 0,434 | 0,941 0,765 0,642 0,560 0,507 | 0,976 0,846 0,729 0,644 0,586 | 0,988 0,899 0,780 0,698 0,637 | |
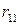
| 0,479 0,441 0,409 | 0,554 0,512 0,477 | 0,631 0,587 0,551 | 0,683 0,636 0,597 | |

| 0,517 0,490 0,467 | 0,576 0,546 0,521 | 0,538 0,605 0,578 | 0,679 0,642 0,615 | |

| 0,462 0,472 0,452 0,438 0,424 0,412 0,401 0,391 0,382 0,374 0,367 0,360 | 0,546 0,525 0,507 0,490 0,475 0,462 0,450 0,440 0,430 0,421 0,413 0,406 | 0,602 0,579 0,559 0,542 0,527 0,514 0,502 0,491 0,481 0,472 0,464 0,457 | 0,641 0,616 0,595 0,577 0,561 0,547 0,535 0,524 0,514 0,505 0,497 0,489 |
Вычисленные для выборки по формулам значения коэффициентов Диксона  сравнивают с принятым (табличным) значением критерия Диксона
сравнивают с принятым (табличным) значением критерия Диксона 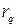 (таблица 3.6.7). Нулевая гипотеза об отсутствии грубой погрешности выполняется, если выполняется неравенство:
(таблица 3.6.7). Нулевая гипотеза об отсутствии грубой погрешности выполняется, если выполняется неравенство:
 . (3.6.12)
. (3.6.12)
Полученные результаты занести в таблицу 3.6.8.
Таблица 3.6.8 – Отчет лабораторной работы
| xi | ||||||||
| mi | ||||||||

| 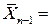
| 
| 
| |||||
| Заключение о грубой погрещности | По критерию "3 σ " | |||||||
| По критерию Смирнова | ||||||||
| По критерию Романовского | ||||||||
| По критерию Ирвина | ||||||||
| По критерию вариационного размаха | ||||||||
| По критерию Диксона |
Рассмотрим пример применения критериев для исключения грубых погрешностей при измерении сопротивления. Полученные результаты представлены в таблице 3.6.9.
Таблица 3.6.9 – Результаты наблюдений
| R, Ом | 3,42 | 3,43 | 3,44 | 3,45 | 3,46 | 3,47 | 3,48 | 3,49 | 3,50 |
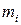
|
Требуется определить, содержит ли результат наблюдения R =3,50 Ом грубую погрешность.
Для графического определения вида закона распределения построим гистограмму. При построении разбиение на интервалы осуществляем таким образом, чтобы измеренные значения оказались серединами интервалов, что показано на рисунке 3.6.1.
По виду гистограммы предположительно идентифицируем опытное распределение нормальным. Вычисляем оценки  и
и 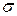 :
:
 Ом;
Ом;
 Ом,
Ом,
где  коэффициент смещения.
коэффициент смещения.

Рисунок 6.1 – Общий вид гистограммы
Решим задачу с помощью критериев, установленных для нормального распределения.
1. Проверка по критерию "3 σ ". Вычислим удаленность подозрительного результата от центра распределения:  Ом.
Ом.
Определим границу погрешности:  Ом.
Ом.
Поскольку  , то можно сделать вывод, что результат
, то можно сделать вывод, что результат 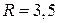 Ом не содержит грубой погрешности.
Ом не содержит грубой погрешности.
2. Проверка по критерию Смирнова "  ". Из таблицы 3.6.2 (n <25) для принятого уровня значимости q =0,05 и объема выборки n =20 находим βk =2,799. Наличие грубой погрешности в результате R =3,50 Ом не подтверждается, так как:
". Из таблицы 3.6.2 (n <25) для принятого уровня значимости q =0,05 и объема выборки n =20 находим βk =2,799. Наличие грубой погрешности в результате R =3,50 Ом не подтверждается, так как:
 .
.
3. Проверка по критерию Романовского. Определяем характеристики распределения без учета подозрительного результата ( ):
):
 Ом.
Ом.
По таблице 3.6.3 находим коэффициент Стьюдента при объеме выборки  и доверительной вероятности P = 0,95; t 0,95 = 2,093. Наличие грубой погрешности подтверждается, т. к.:
и доверительной вероятности P = 0,95; t 0,95 = 2,093. Наличие грубой погрешности подтверждается, т. к.:
 .
.
4. Проверка по критерию Ирвина. Для полученных экспериментальных данных определяют коэффициент по формуле:
 .
.
Затем этот коэффициент сравнивается с табличным значением  , значения которого приведены в таблице 3.6.4. Т. к.
, значения которого приведены в таблице 3.6.4. Т. к.  , то нулевая гипотеза не подтверждается, т. е. результат
, то нулевая гипотеза не подтверждается, т. е. результат 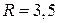 Ом не содержит грубой погрешности.
Ом не содержит грубой погрешности.
5. Проверка по критериювариационного размаха. Для его использования определяют размах вариационного ряда упорядоченной совокупности наблюдений  :
:
 .
.
Выполняем проверку по следующему неравентсву:
 ,
,
где  выборочное среднее арифметическое значение, вычисленное после исключения предполагаемого промаха (для
выборочное среднее арифметическое значение, вычисленное после исключения предполагаемого промаха (для 
 );
);
 критериальное значение (таблица 3.6.5).
критериальное значение (таблица 3.6.5).
Условие выполняется:  .
.
Т. е. результат 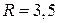 Ом не содержит грубой погрешности.
Ом не содержит грубой погрешности.
7. Проверка по критерию Диксона. При использовании критерия вычисляют коэффициент Диксона (наблюдаемое значение критерия) для проверки наибольшего или наименьшего экстремального значения в зависимости от числа измерений. В таблице 3.6.6 приведены формулы для вычисления коэффициентов.
Для нашего случая:  .
.
Вычисленные для выборки по формулам значения коэффициентов Диксона  сравнивают с принятым (табличным) значением критерия Диксона
сравнивают с принятым (табличным) значением критерия Диксона 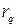 (таблица 6.8). Нулевая гипотеза об отсутствии грубой погрешности выполняется, если выполняется неравенство
(таблица 6.8). Нулевая гипотеза об отсутствии грубой погрешности выполняется, если выполняется неравенство  .
.
Если 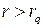 , то результат признается грубой погрешностью и исключается из дальнейшей обработки. В нашем случае:
, то результат признается грубой погрешностью и исключается из дальнейшей обработки. В нашем случае:  , т.е. грубая погрешность отсутствует.
, т.е. грубая погрешность отсутствует.
Поскольку большинство критериев (6 из 7) показали отсутствие грубой погрешности, то результат наблюдения можно оставить в выборке.
Date: 2016-05-18; view: 1223; Нарушение авторских прав