
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Методические рекомендации к лабораторному занятию. 1. Измерить размеры физической величины заданных объектов
|
|
1. Измерить размеры физической величины заданных объектов. Полученную выборку представить в виде таблицы. Определить предельные значения выборки (Х max, Х min). Найти размах варьирования по формуле:
 . (3.2.1)
. (3.2.1)
Задаваясь числом интервалов (K –5…11), определить величину интервала:
 . (3.2.2)
. (3.2.2)
2. Найти границы интервалов выборки можно следующим образом:
- границы 1 интервала –  ;
;
- границы 2 интервала –  ;
;
- границы k интервала –  .
.
В каждый интервал включаются размеры, лежащие в пределах от наименьшего значения интервала включительно до наибольшего значения интервала, исключая его. В таблице 3.2.1 при помощи черточек сделать подсчет частот по интервалам.
Таблица 3.2.1 – Подсчет частот эмпирического распределения
| Интервалы | Подсчет частот fi | Частота fi | |
| от | до | ||
3. Составить таблицу 3.2.2 (эмпирическое распределение X) и построить эмпирическую кривую распределения (рисунок 3.2.1). Значения середин интервалов и частостей находятся по формулам 3.2.3 и 3.2.4 соответственно.
 , (3.2.3)
, (3.2.3)
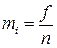 , (3.2.4)
, (3.2.4)
где n – общее число наблюдаемых значений случайной величины.
Таблица 3.2.2 – Эмпирическое распределение
| Интервалы | Середина интервала Xi | Частота fi | Частость mi | |
| от | до | |||

Рисунок 3.2.1 – Эмпирическая кривая распределения
4. Для вычисления статистических характеристик распределения предварительно заполнить вспомогательную таблицу 3.2.3 для вычисления среднего арифметического  и среднего квадратического σ выборки
и среднего квадратического σ выборки
Таблица 3.2.3 – Вспомогательная таблица для определения  и σ
и σ
| Середина интервала | Частость mi |  
| 
| 
| 
|
∑= 
| ∑= 
|
5. Определить аргументы функции Лапласа в зависимости от значений заданных предельных отклонений: верхнего В и нижнего Н по формулам:
 ,
,  . (3.2.5)
. (3.2.5)
6. Определить вероятность попадания результатов измерений в поле допускаемых значений физической величины по формуле:
 , (3.2.6)
, (3.2.6)
где  .
.
Пример. Из текущей продукции автомата, обрабатывающего ролики, d =20 g 10 была взята выборка объемом n =100шт. Требуется определить вероятность получения размеров в пределах допуска.
Таблица 3.2.4 – Отклонения от номинального размера диаметров роликов
-0,07 -0,03 -0,04 -0,08 -0,03 -0,08 -0,09 -0,10 -0,10 -0,10
-0,13 -0,08 -0,06 -0,04 -0,04 -0,03 -0,04 -0,07 -0,11 -0,12
-0,03 -0,07 -0,08 -0,11 -0,05 -0,05 -0,07 -0,03 -0,09 -0,10
-0,05 -0,12 -0,07 -0,06 -0,08 -0,11 -0,08 -0,12 -0,03 -0,10
-0,11 -0,14 -0,13 -0,08 -0,12 -0,07 -0,09 -0,10 -0,11 -008
-0,08 -0,05 -0,11 -0,07 -0,05 -0,08 -0,10 -0,09 -0,09 -0,02
-0,06 -0,12 -0,05 -0,07 -0,11 -0,05 -0,09 -0,03 -0,11 -0,09
-0,11 -0,06 -0,07 -0,06 -0,06 -0,12 -0,10 -0,08 -0,09 -0,01
-0,05 -0,07 -0,06 -0,05 -0,08 -0,09 -0,14 -0,09 -0,08 -0,09
-0,07 -0,06 -0,06 -0,12 -0,05 -0,03 -0,10 -0,09 -0,09 -0,08
Находим Xmax = -0,01;
Xmin = - 0,14.
Определяем размах варьирования:
R = Xmax – Xmin =0,13 мм.
Определяем величину интервала:
 .
.
Заполняем таблицу подсчета частот эмпирического распределения.
Таблица 3.2.5 – Подсчет частот эмпирического распределения
| Интервалы | Подсчет частот fi | Частота fi | |
| от | до | ||
| -0,14 -0,12 -0,10 -0,08 -0,06 -0,04 -0,02 | -0,12 -0,10 -0,08 -0,06 -0,04 -0,02 -0,01 | III IIIIIIIIIIIIIIII IIIIIIIIIIIIIIIIIIIIII IIIIIIIIIIIIIIIIIIIIIIIII IIIIIIIIIIIIIIIIIII IIIIIIIIIIIII II | |
| ∑fi =100 |
Таблица 3.2.6 – Эмпирическое распределение
| Интервалы | Середина интервала Xi | Частота fi | Частость mi | |
| От | До | |||
| -0,14 -0,12 -0,10 -0,08 -0,06 -0,04 -0,02 | -0,12 -0,10 -0,08 -0,06 -0,04 -0,02 -0,00 | -0,13 -0,11 -0,09 -0,07 -0,05 -0,03 -0,01 | 0,03 0,16 0,22 0,25 0,19 0,13 0,02 | |
| ∑fi =100 | ∑mi =1 |
Здесь Xi определяется по формуле 3.2.3.
тi определяется по формуле 3.2.4.
Вычерчиваем эмпирическую кривую распределения.

Рисунок 3.2.2 – Эмпирическая кривая распределения заданной выборки
Таблица 3.2.7 – Определение  и σ:
и σ:
| Середина интервала | Частость mi |  
| 
| 
| 
|
| -0,13 -0,11 -0,09 -0,07 -0,05 -0,03 -0,01 | 0,03 0,16 0,22 0,25 0,19 0,13 0,03 | -0,0039 -0,0176 -0,0198 -0,0178 -0,0095 -0,0039 -0,0003 | 0,058 0,038 0,018 -0,002 -0,022 -0,042 -0,062 | 0,0033 0,0014 0,0003 0,000004 0,0005 0,0017 0,0038 | 0,000099 0,00022 0,00006 0,000001 0,000095 0,00022 0,00011 |
| ∑=-0,0725 ∑=0,00784 |
Искомые величины  и σ определяются соответственно как суммы третьего и шестого столбца таблицы 3.2.7.
и σ определяются соответственно как суммы третьего и шестого столбца таблицы 3.2.7.
 ,
,
 .
.
По таблицам для d 20 g 10 определяем: es = -7мкм; ei = -91 мкм.

Ф (2,32) – Ф (-0,68)= Ф (2,32) + Ф (0,68)=0,4898+0,2517=0,7415.
Таким образом, вероятность получения размеров в пределах допуска составляет 74,1%.
Date: 2016-05-18; view: 393; Нарушение авторских прав