
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Общая схема исследования функции
|
|
1. Нахождение области определения.
2. Исследование функции на четность, нечетность и периодичность.
3. Нахождение точек пересечения графика функции с осями координат. Точки пересечения с осью ОХ: ( ,0), где
,0), где  - решение уравнения f(x)= 0. Точки пересечения с осью ОY: (0, f( 0 )).
- решение уравнения f(x)= 0. Точки пересечения с осью ОY: (0, f( 0 )).
4. Нахождение промежутков знакопостоянства функции. Промежутки знакопостоянства функции – промежутки из области определения функции, где функция принимает положительные или отрицательные значения, т.е. f(x) >0 или f(x) <0.
5. Нахождение производной функции, области определения производной, критических точек.
6. Нахождение промежутков возрастания, убывания, точек экстремума.
7. Нахождение промежутков выпуклости функции и точек перегиба.
1. Исследование поведения функции на бесконечности и в окрестности точек разрыва. Нахождение вертикальных, горизонтальных, наклонных асимптот.
2. Построение графика (при необходимости нужно найти значения функции в дополнительных точках).
РЕШЕНИЕ ЗАДАЧ
ПРИМЕР 1. Исследовать функцию f(x) =  и построить график;
и построить график;
1. D (f) =ℝ  .
.
2. f(-x) 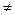 f(x) и f(-x)
f(x) и f(-x) 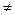 -f(x), следовательно, f(x) - функция общего вида.
-f(x), следовательно, f(x) - функция общего вида.
3. Точки пересечения с осями координат:
OX: y= 0, 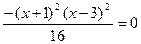 , x = -1, x =3; (-1,0), (3,0);
, x = -1, x =3; (-1,0), (3,0);
OY: x= 0, f( 0 ) = -  ; (0,-
; (0,-  ).
).
4. Промежутки знакопостоянства:
f(x)< 0 при x  (-
(-  ,-1)
,-1)  (-1,3)
(-1,3)  (3,+
(3,+  )
)
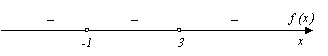
5. Найдем производную функции, промежутки возрастания, убывания, точки экстремума
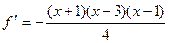
Область определения производной функции: D ( ) = R.
) = R.
 = 0, x= -1, x= 3, x= 1.
= 0, x= -1, x= 3, x= 1.
f(x) возрастает на промежутках (-  ,-1] и [1,3];
,-1] и [1,3];
f(x) убывает на промежутках [-1,1] и [3,+  ).
).
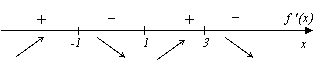
Точки экстремума:  , f( 1 ) = -1;
, f( 1 ) = -1;
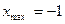 , f( -1 ) = 0;
, f( -1 ) = 0;
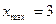 , f( 3 ) = 0;
, f( 3 ) = 0;
6. Найдем промежутки выпуклости, вогнутости функции и ее точки перегиба.
После преобразований получим, что
 .
.
Обозначим 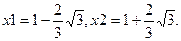
Таким образом, получим
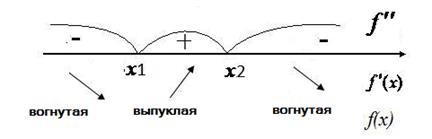
7.
1.Вертикальных асимптот нет, так как f(x) определена(и непрерывна) на всей числовой прямой.
Исследуем поведение функции на бесконечности.
2. Исследуем на наличие горизонтальных асимптот.

 f(x) =
f(x) = 
 =
=  ,
,
 f(x) =
f(x) = 
 =
=  .
.
Таким образом, горизонтальные асимптоты отсутствуют.
3. Исследуем на наличие наклонных асимптот.
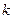 =
= 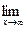
 =
= 
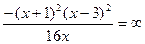 .
.
Таким образом, наклонные асимптоты отсутствуют.
8. Дополнительные точки: f( -3 ) = -9, f( 5 ) = -9.
9. Построим график функции:

Рис.2.16
УПРАЖНЕНИЯ
Исследовать и построить графики следующих функций:
3.1. f(x)= 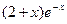 ;
;
3.2. f (x)= 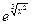 ;
;
3.3. f(x)=  ;
;
3.4. f(x)= 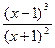 ;
;
3.5. f(x)=  ;
;
3.6. f(x)= 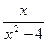 ;
;
3.7. f (x)=  ;
;
3.8. f (x)= 1+  ;
;
3.9. f (x)= 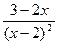 ;
;
3.10. f(x)= 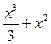 .
.
Ответы к упражнениям
3.1. 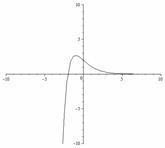 3.2.
3.2.  3.3.
3.3. 
3.4. 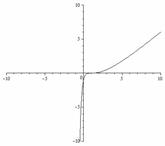 3.5.
3.5. 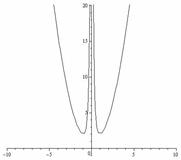 3.6.
3.6. 
3.7. 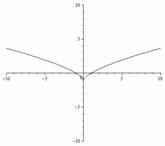 3.8.
3.8.  3.9.
3.9. 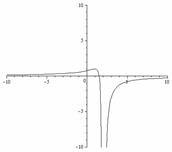
3.10. 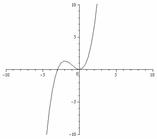
Date: 2016-05-17; view: 584; Нарушение авторских прав