
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Задания для контрольных работ. Исследовать функцию и построить её график:
|
|
Исследовать функцию и построить её график:
1. 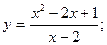
2. 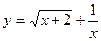 ;
;
3. 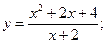
4. 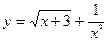 ;
;
5. 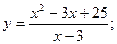
6. 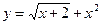 ;
;
7. 
8. 
9. 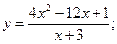
10.  ;
;
11. 
12. 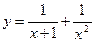 ;
;
13. 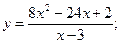
14. 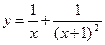 ;
;
15. 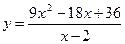 ;
;
16. 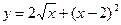 ;
;
17. 
18. 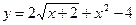 ;
;
19. 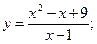
20. 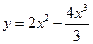 +
+ 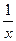 ;
;
21. 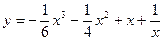 ;
;
22. 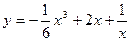 ;
;
23.  ;
;
24. 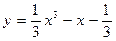 +
+ 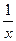 ;
;
25.  +
+ 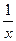 ;
;
26.  ;
;
27.  ;
;
28. 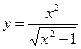 ;
;
29. 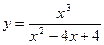 ;
;
30. 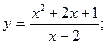
31. 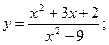
32. 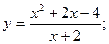
33. 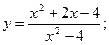
34. 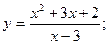
35. 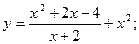
36. 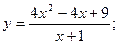
37. 
38. 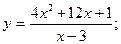
39. 
40. 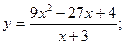
41. 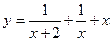 ;
;
42. 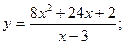
43. 
44.  ;
;
45. 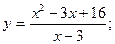
46. 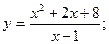
47. 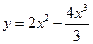 -
- 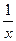 ;
;
48.  ;
;
49. 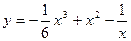 ;
;
50. 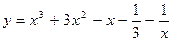 ;
;
51. 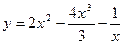 ;
;
52. 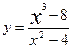 ;
;
53. 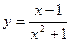 ;
;
54. 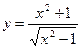 ;
;
55. 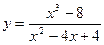 .
.
Задания с экономическим содержанием
1. Фирма «Конфетти», занимающаяся продажей офисной мебели, провела опрос дилеров и получила следующие сведения о спросе Q на свою продукцию в зависимости от цены Р:
| Р, тыс. руб. | ||||
| Q, тыс. шт. |
Определить область определения и множество значения функции спроса.
2. Величина подоходного налога h с физического лица в зависимости от его годового дохода q представлена функцией h(q):
| Годовой доход q, тыс. руб. | Величина налога h(q), тыс. руб. |

| 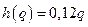
|
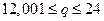
| 
|
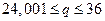
| 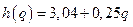
|

| 
|
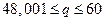
| 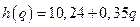
|

| 
|
Найти множество значений и область определения данной функции.
3. Построить график таблично заданной функции:
| Цена пачки макарон, руб. | ||||||||
| Количество проданных за день пачек, шт. |
4. Постоянные издержки F (не зависящие от числа x единиц произведенной продукции) составляет 125 тыс. руб. в месяц, а переменные издержки V(x) (пропорциональные x) – 700 руб. за каждую единицу продукции. Цена единицы продукции равна 1200 руб. Найти объем продукции x, при котором прибыль равна: а) нулю (точка безубыточности); б) 105 тыс. руб. в месяц.
Указание: Общие издержки находятся из суммы постоянных и переменных издержек, прибыль равна разности выручки и общих издержек.
5. Фирма купила новый станок для обработки древесины стоимостью 250 тыс. руб. Полагая зависимость стоимости станка от времени эксплуатации линейной, найти его стоимость через 6 лет. Ежегодная норма амортизации составляет 7 %.
6. Банк выплачивает ежегодно 5 % годовых (сложный процент). Определить: а) размер вклада через три года, если первоначальный вклад составляет 10 тыс. руб.; б) размер первоначального вклада, при котором через четыре года вклад (вместе с начисленными процентами) составит 10 тыс. руб.
Указание: Размер вклада 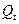 через
через 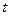 лет определяется по формуле
лет определяется по формуле 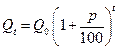 , где
, где 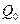 - первоначальный вклад;
- первоначальный вклад; 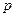 - годовая процентная ставка.
- годовая процентная ставка.
7. Функция суточного спроса 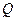 на мороженое (тыс. шт.) в зависимости от цены
на мороженое (тыс. шт.) в зависимости от цены 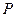 за одну порцию (руб.) имеет вид
за одну порцию (руб.) имеет вид  . Эффективная область «работы» этой формулы от 1 до 9 руб. При какой цене за порцию мороженого совокупная выручка будет наибольшей?
. Эффективная область «работы» этой формулы от 1 до 9 руб. При какой цене за порцию мороженого совокупная выручка будет наибольшей?
Указание: Совокупная выручка определяется по формуле 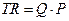 , где
, где 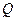 - количество реализованных порций мороженого (тыс. шт.);
- количество реализованных порций мороженого (тыс. шт.); 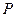 - цена за одну порцию (руб.).
- цена за одну порцию (руб.).
8. Если собрать урожай в начале августа, то с каждой сотки можно получить 200 кг раннего картофеля и реализовать его по 12 руб. за килограмм. Отсрочка уборки на каждую неделю ведет к увеличению урожайности на 50 кг с одной сотки, но цена картофеля за килограмм при этом падает на 2 руб. Когда следует собрать картофель, чтобы доход от его продажи был максимальным, если срок уборки картофеля составляет 5 недель?
9. Издержки производства некоторого товара равны  ; спрос на товар определяется функцией
; спрос на товар определяется функцией 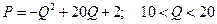 . Найти объем продукции
. Найти объем продукции 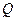 , максимизирующий прибыль.
, максимизирующий прибыль.
10. Функция издержек имеет вид 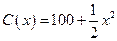 , а доход при производстве
, а доход при производстве  единиц товара определяется следующим образом:
единиц товара определяется следующим образом:
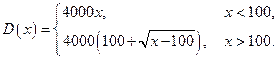
Определить максимальное для производителя значение выпуска 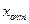 .
.
Ответы: 1. Область определения – значения Р, множество значений – величины Q. 2. Область определения и множество значений – все положительные действительные числа. 4. а) 250 ед., б) 460 ед. 5. 145 тыс. руб. 6. а) 11,576 руб.; б) 8227 руб. 7. 4руб. 8. через 1 неделю 9. 13 10. 200 ед.
Тест
Вариант 1
- Выяснить, какие функции являются непрерывными, но не дифференцируемыми в точке
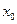 :
:
1) 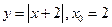
2) 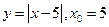
3) 
2. Выяснить, какие из функций являются дифференцируемыми в точке 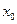 =1:
=1:
1) 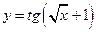
2) 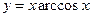
3) 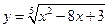
3. Определить характер разрыва функции 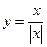 :
:
1) х=0 – точка разрыва первого рода
2) х=0 – точка разрыва второго рода
3) х=0 – точка устранимого разрыва
4) точек разрыва нет
4. Найти точки экстремума функции 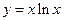
1) 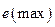
2) 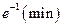
3) 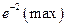
4) 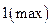
5. Найти точки экстремума функции 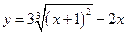
1) 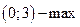
2) 
3) 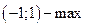
4) 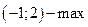
6. Найти абсциссы точек перегиба графика функции 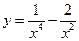
1) 
2) 
3) 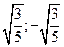
4) 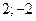
7. Найти асимптоты графика функции 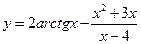
1) 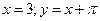
2) 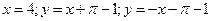
3) 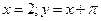
4) 
8. Выяснить, какие из приведенных утверждений являются неверными:
1) в точке экстремума производная функции равна 0 или не существует
2) в точке экстремума функция меняет знак
3) в точке экстремума производная функции меняет знак
4) в точке, в которой производная равна нулю или не существует, может не быть экстремума
9. Выяснить, какие из перечисленных функций непрерывны в точке x=0:
1) 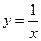 2)
2) 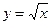 3)
3) 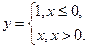 4)
4) 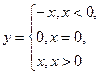
10. Указать область определения функции 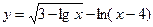 :
:
1)(0;3] 2)(4;1000] 3)(3;1000] 4) [1000;+  )
)
11. Выяснить, какие функции являются ограниченными:
1) 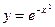 2)
2) 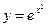 3)
3)  4)
4) 
12.Выяснить, какие функции являются сложными:
1) 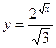 2)
2) 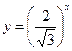 3)
3) 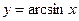 4)
4) 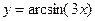
13. Выяснить, какие функции являются нечетными:
1)  2)
2) 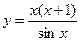 3)
3) 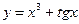 4)
4) 
14. Среди перечисленных функций горизонтальные асимптоты имеют функции:
1) 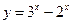 2)
2) 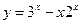 3)
3)  4)
4) 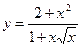
15. Среди перечисленных функций вертикальные асимптоты имеют функции:
1)  2)
2) 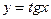 3)
3)  4)
4) 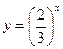
16. Указать промежутки возрастания функции 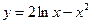 :
:
1) 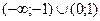 2)
2) 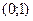 3)
3) 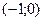 4)
4) 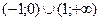
17. Среди перечисленных функций убывает на всей области определения функция:
1)  2)
2)  3)
3)  4)
4) 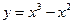
 18. Функция у = f (x) определена на промежутке (– 6; 4). График ее производной изображен на рисунке. Укажите точку минимума функции у = f (x) на этом промежутке.
18. Функция у = f (x) определена на промежутке (– 6; 4). График ее производной изображен на рисунке. Укажите точку минимума функции у = f (x) на этом промежутке.
19. Составить уравнение касательной к графику функции 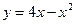 в точках пересечения с осью Ox.
в точках пересечения с осью Ox.
20.Найти наименьшее и наибольшее значение функции 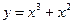 на отрезке [-1;2].
на отрезке [-1;2].
21. Указать промежутки выпуклости функции 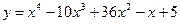 :
:
1) 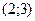 2)
2) 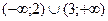 3)
3) 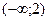 4)
4) 
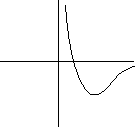
22. Выяснить, какой из графиков на рисунке есть график функции  :
:
1) 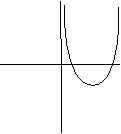 2)
2) 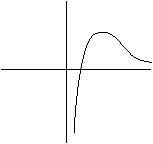 3)
3)  4)
4) 
23.Количество целых значений x из области определения функции  равно
равно
1)6 2)3 3)5 4)4
 24.Дан график функции
24.Дан график функции 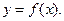
Тогда верны утверждения
1)  при
при 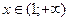
2)  при
при 
3) 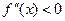 при
при 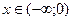
4) x =2, x =4 –точки перегиба
5) x =0—точка перегиба
25.Даны функции спроса 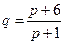 и предложения
и предложения 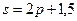 , где p—цена товара. Тогда равновесная цена равна
, где p—цена товара. Тогда равновесная цена равна
1)3,5 2)2,25 3)4,5 4)1
26. Найти область значений функции 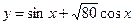 .
.
27. Выяснить, какие из функций заданы неявно
1) 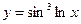 2)
2) 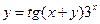 3)
3) 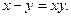
28. Укажите верные утверждения для функции 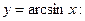
1)монотонная; 2)ограниченная; 3)неограниченная; 4)четная; 5)нечетная; 6)общего вида; 7)явная; 8)неявная; 9)сложная.
Вариант 2
- Выяснить, какие функции являются непрерывными, но не дифференцируемыми в точке
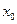 :
:
1) 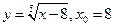
2) 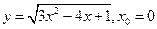
3) 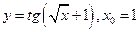
2. Выяснить, какие из функций являются дифференцируемыми в точке 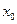 =1:
=1:
1) 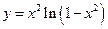
2) 
3) 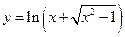
3. Определить характер разрыва функции  :
:
1) х=7 – точка разрыва первого рода
2) х=7 – точка разрыва второго рода
3) х=7 – точка устранимого разрыва
4) точек разрыва нет
4. Найти точки экстремума функции 
1) 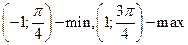
2) 
3) экстремумов нет
5. Найти точки экстремума функции 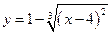
1) 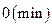
2) экстремумов нет
3) 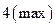
4) 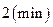
6. Найти абсциссы точек перегиба графика функции 
1) 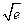
2) 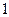
3) 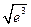
4) 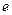
7. Найти асимптоты графика функции 
1) 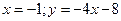
2) 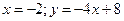
3) 
4) 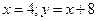
8. Следующие из перечисленных утверждений являются всегда верными:
1) в точке перегиба всегда существует конечная первая производная
2) в точке перегиба существует конечная вторая производная
3) точка перегиба является точкой экстремума первой производной функции
4) точка перегиба является точкой экстремума второй производной функции
9. Выяснить, какие из перечисленных функций непрерывны в точке x=0:
1) 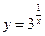 2)
2) 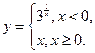 3)
3)  4)
4) 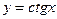
10. Указать область определения функции 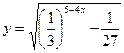 +
+ 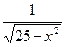 :
:
1) (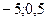 ] 2) (-
] 2) (- 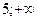 ) 3) (
) 3) (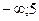 ) 4) [
) 4) [ 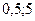 )
)
11.Выяснить, какие функции являются ограниченными:
1) 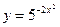 2)
2) 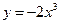 3)
3) 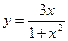 4)
4) 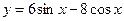
12.Выяснить, какие функции являются сложными:
1) 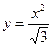 2)
2) 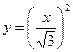 3)
3) 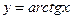 4)
4) 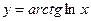
13. Выяснить, какие функции являются четными:
1) 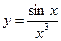 2)
2)  3)
3) 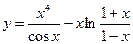 4)
4) 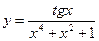
14. Среди перечисленных функций горизонтальные асимптоты имеют функции:
1) 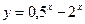 2)
2) 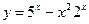 3)
3) 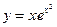 4)
4) 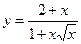
15. Среди перечисленных функций вертикальные асимптоты имеют функции:
1) 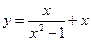 2)
2) 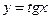 3)
3) 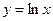 4)
4) 
16.Найти промежутки, на которых возрастает функция 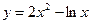 (x>0):
(x>0):
1)  2)
2) 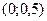 3)
3)  4)
4) 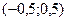
17. Среди перечисленных функций возрастает на всей области определения функции:
1) 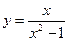 2)
2) 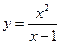 3)
3)  4)
4) 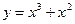
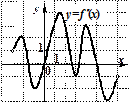 18.Функция
18.Функция  определена на промежутке (–3; 7). График ее производной изображен на рисунке. Укажите число точек минимума функции
определена на промежутке (–3; 7). График ее производной изображен на рисунке. Укажите число точек минимума функции  на промежутке (–3; 7).
на промежутке (–3; 7).
19. Составить уравнение касательной к графику функции 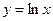 в точке пересечения с осью Ox:
в точке пересечения с осью Ox:
20.Найти наименьшее и наибольшее значение функции 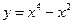 на отрезке [-1;2]:
на отрезке [-1;2]:
21. Указать промежутки выпуклости функции 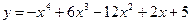 :
:
 1)
1) 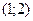 2)
2)  3)
3) 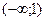 4)
4) 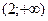
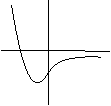
22. Выяснить, график какой функции изображен на рисунке:
1) 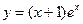 2)
2) 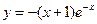 3)
3)  4)
4) 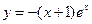
23.Количество натуральных значений x из области определения функции  равно
равно
1)6 2)3 3)5 4)4
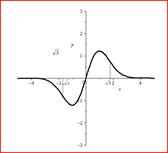 24.Дан график функции
24.Дан график функции 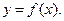
Тогда верны утверждения
1)  при
при 
2)  при
при 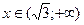
3) 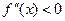 при
при 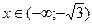
4) x = 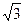 , x =
, x = 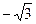 –точки перегиба
–точки перегиба
5) x =1-- точка перегиба
25.Даны функции спроса 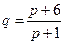 и предложения
и предложения 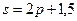 , где p—цена товара. Тогда равновесный объем «спроса-предложения»(q=s) равен
, где p—цена товара. Тогда равновесный объем «спроса-предложения»(q=s) равен
1)1 2)6 3)3,5 4)10,5
26. Найти область значений функции 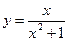 .
.
27.Выяснить, какие из функций заданы неявно
1) 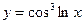 2)
2) 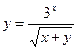 3)
3) 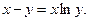
28. Укажите верные утверждения для функции 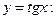
1)монотонная; 2)ограниченная; 3)неограниченная; 4)четная; 5)нечетная; 6)общего вида; 7)явная; 8)неявная; 9)сложная.
Date: 2016-05-17; view: 1549; Нарушение авторских прав