Приемы и методы детерменированного факторного анали

Детерминированный факторный анализ проводится в несколько этапов: 1построение экономически обоснованной (с позиций факторного анализа) детерминированной факторной модели; выбор приема анализа и подготовка условий для его выполнения; 2 реализация счетных процедур; 3 формулирование выводов.

По виду (принципу построения) различают аддитивные (сумма факторов), мультипликативные (произведение фактров), кратные (частное) и смешанные модели факторных систем.

При моделировании факторных систем могут использоваться следующие методы: расчленение; удлинение; формальное разложение; расширение; сокращение.

В детерминированном факторном анализе используются следующие методы: цепной подстановки, индексный, абсолютных разниц, относительных разниц, пропорционального деления, долевого участия, интегральный, логарифмирования и др. Первые четыре способа основаны на методе элиминирования. Элиминировать — значит устранить, отклонить, исключить воздействие всех факторов на величину результативного показателя, кроме одного. Этот метод исходит из того, что все факторы изменяются независимо друг от друга: сначала изменяется один, затем изменяются два, затем три и т.д. при неизменности остальных. Это позволяет определить влияние каждого фактора на величину исследуемого показателя в отдельности.

Наиболее универсальным является способ цепной подстановки. Он используется для расчета влияния факторов во всех типах детерминированных факторных моделей: аддитивных, мультипликативных, кратных и смешанных (комбинированных).

y = f (a,b,c,d) (1.28)

y = f (a1,b1,c1,d1) - f (a0,b0,c0,d0) (1.29)

ya = f (a1,b0,c0,d0) - f (a0,b0,c0,d0) (1.30)

yb = f (a1,b1,c0,d0) - f (a1,b0,c0,d0) (1.31)

yc = f (a1,b1,c1,d0) - f (a1,b1,c0,d0) (1.32)

yd = f (a1,b1,c1,d1) - f (a1,b1,c1,d0) (1.33)

y = ya + yb + yc + yd (1.34

Способ абсолютных разниц. Изменение результативного показателя за счет каждого фактора способом разниц определяется как произведение отклонения изучаемого фактора на базисное или отчетное значение другого фактора в зависимости от выбранной последовательности подстановки:

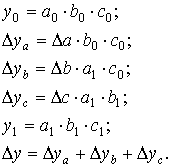
Метод относительных разниц применяется для измерения влияния факторов на прирост результативного показателя только в мультипликативных и комбинированных моделях мультипликативно- аддитивного типа. Здесь используются относительные приросты факторных показателей, выраженные в виде коэффициентов или процентов.

Для мультипликативных моделей типа у = а. в. с методика анализа следующая:

· находят относительное отклонение каждого факторного показателя:

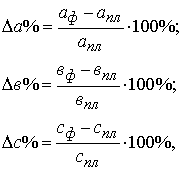
· определяют отклонение результативного показателя у за счет каждого фактора

Индексный метод основан на относительных показателях динамики, пространственных сравнений, выполнения плана, выражающих отношение факторного уровня анализируемого показателя в отчетном периоде к его уровню в базисном периоде С помощью агрегатных индексов можно выявить влияние различных факторов на изменение уровня результативных показателей в мультипликативных и кратных моделях.

Интегральный способ применяется для измерения влияния факторов в мультипликативных, кратных и смешанных моделях кратно-аддитивного типа. Его использование позволяет получать более точные результаты расчета влияния факторов по сравнению со способами цепной подстановки, абсолютных и относительных разниц и избежать неоднозначной оценки влияния факторов.

Метод логарифмирования применяется для измерения влияния факторов в мультипликативных моделях. общий прирост результативного показателя распределяется по факторам пропорционально отношениям логарифмов факторных индексов к логарифму результативного показателя. Dу_а=DУ_общ*lgDa/lgDY

Date: 2016-01-20; view: 438; Нарушение авторских прав