Главная Случайная страница


Полезное:

Как сделать разговор полезным и приятным Как сделать объемную звезду своими руками Как сделать то, что делать не хочется? Как сделать погремушку Как сделать так чтобы женщины сами знакомились с вами Как сделать идею коммерческой Как сделать хорошую растяжку ног? Как сделать наш разум здоровым? Как сделать, чтобы люди обманывали меньше Вопрос 4. Как сделать так, чтобы вас уважали и ценили? Как сделать лучше себе и другим людям Как сделать свидание интересным?


Категории:

АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника






Прямая на плоскости

⇐ ПредыдущаяСтр 20 из 64Следующая ⇒

 


 

 

M0(x0,y0), U(m,n) M(x,y)-произвольная

MÎs<=>M0M--||u--<=> M0M--=t*u--, t-число

Параметрическое уравнение прямой: {x-x0=tm, y-y0=tn

Каноническое уравнение: (x-x0)/m=(y-y0)/n

A(x-x0)+B(y-y0)=(Am+Bn)t

A(x-x0)+B(y-y0)=0;

Ax+By-(Ax0+By0)=0; (Ax0+By0)=C;

Ax+By+C=0-общее ур-е (алг-ая линия 1 порядка)

x/a+y/b=1-ур-е в отрезках:

 

 


y=-Ax/B-C/B,B¹0;=>y=kx+b

-A/B=k-угловой коэф-т=tga

OP=p; g=(xÙn);

xcosg+ysing-p=0-норм. ур-е.

 
 

 


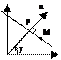Ax+By+C=0-явл. норм-ым, если A2+B2=1;

RAx+Rby+RC=0;

(AR)2+(BR)2=1; ;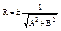

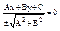(приводим к нормальному виду)

Афин. задачи:

·Прямая проходящая через две точки. Дано: M0(x0y0) M1(x1y1)

Уравнение прямой через одну точку: A(x-x0)+B(y-y0)=0(s)

sÎM1 A(x1-x0)+B(y1-y0)=0; Получили ур-е с неизв. A и B=>A=y1-y0, B=x1-x0;

найденные A и B подставим (x-x0)(y1-y0)-(y-y0) (x1-x0)=0;

(x-x0)/(x1-x0)=(y-y0)/(y1-y0)-искомое ур-е.

·Общая точка двух прямых. Дано: A1x+B1y+C1=0 (s1), A2x+B2y+C2=0 (s2);

Реш. {A1x+B1y+C1=0 A2x+B2y+C2=0;

D= =A1B2-A2B1; Dx= =B1C2-B2C1; Dy= =A2C1-A1C2;

; ;

1°D¹0=>s1Çs2=>k(x;y) ; ;

2°D=0,Dx¹0,Dy¹0 ó реш. нет ó s1||s2

3°D=Dx=Dy=0ó¥ реш.Ûs1=s2;

Метрические задачи:

·Угол между двумя прямыми:

 

Дано: y=k1x+b1(s1), y=k2x+b2(s2)

Найти: tgj, j(s1Ùs2);

По т. Шаля: (xÙs2)+ (s1Ùs2)= (xÙs2)+360°n

a1+j=a2+360°nÞj=(a2-a1)+360°n

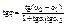
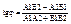k1=tga1; k2=tga2=> => =>(1)уcловие параллельности двух прямых s1||s2ók1=k2 или A1B2-A2B1=0óA1/A2=B1/B2. (2)s1^s2ój=90°=>1+k1k2=0; k1=-1/k2 или A1A2+B1B2=0;

·Расстояние от точки до прямой:

 

 

При s: xcosg+ysing-p; M1(x1,y1);

|d|= |xcosg+ysing-p|

при s:Ax+By+C=0;


⇐ Предыдущая15161718192021222324Следующая ⇒





Date: 2016-02-19; view: 364; Нарушение авторских прав


mydocx.ru - 2015-2025 year. (0.093 sec.) Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав - Пожаловаться на публикацию