Тригонометрич. ряд Фурье

Пусть ф. f(x) непрер. и периодич. с периодом 2p и разлагается в равномерно сходящийся на всей оси числ. прямой ряд, вида .Первый член ряда записан в такой форме для техн удобства. Поскольку данный ряд составлениз непрер. ф-й и равном-но сход-я, то его можем почленно интегрировать. Возьмём интегралы от обеих частей в указанном равенстве на отрезке [-p,p]. В силу ортогональности тригон-х ф-й все интегралы, кроме первого при коэф-е а₀/2 будут равны нулю. Т.е. (*). Домножим обе части (*) на cos(nx) и почленно проинтегрируем. В силу ортогональности тригоном. ф-й все интегралы, кр. интеграла вида a_np® . Аналогично, домножим обе части (*) на sin(nx) и проинтегрировав с учётом ортогон-ти тригон. ф-й найдём: 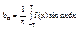. Мы получили ф-лы по кот-м опред-ся коэф-ты указ. тригоном. ряда, причём они опред-ся однозначно. Эти коэф-ты: a₀,a_n,b­_n наз. коэф-ми Фурье. Ф-лы по которым они вычисл. наз. формулами Ейлера-Фурье, а сам ряд, в который разлагается данная ф-я f(x) и коэф-ты которые опр-ся по этим формулам наз-т тригонометрическим рядом Фурье. Нами доказана следующая теорема: если f(x) непрер. и периодич. с периодом T=2p, разлагается в равномерно сходящ-ся тригоном. ряд, то этот ряд будет рядом Фурье (т.е. коэф-ты опр-ся указ-ми фор-ми). Если указ. формулы инт. Для f(x), то её ряд Фурье м.б. построен формально. Будет ли он сходится? и именно в данной ф-и? Для ответа нужны достат признаки. Среди множества достат признаков мы укажем 1, который имеет место для кусочно-диф-мой ф-и: Опр: ф-я f(x) наз. косочно-диф-ой на [a,b], если этот отрезок м-о разбить на конеч. число частей: a=a₀<a₁<…<a_i<…<a_n=b. На каждом из к-х ф-я явл. кусочно-диф-ой, и на концах [a,b] f(x) имеет конечные одностор. пределы-f(a_i,+0), f”(a_i,+0); f(a_i+1,-0), f’(a_i+1,-0)

Признак (Дирихле).

Для кусочно-диф-ой ф-и f(x) с T=2p, её тригоном. ряд Фурье в кажд. т. x=x₀ сх-ся и имеет сумму . Очевидно, что если f(x) в т. x=x₀ непрерывна, то S₀=f(x₀)

Ряды Фурье для чётных и нечёт. ф-й с периодом T=2p.

Пусть ф-я y=f(x)-чётн. т.е. f(-x)=f(x)

; ; ;

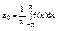Если f(x) чётная, то в её разложении в ряд Фурье все компоненты b_n=0 и говорят, что разложение проводят по косинусам. Получаем: если f(x)-четн., то . Аналогично расужд, если f(x)-нечёт.,

то: ; ; 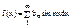, где 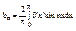; Пр: разложить ф-ю f(x)=x, xÎ[0,p] в ряд Фурье по cos.

1.

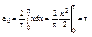, = . 2. разложить по sin.

a₀=0;a_n=0;(рис) . . Замечание: 1. чёт. ф-и разлож. в ряд Фурье т-о по cos т.е. (b_n=0), а нечёт. ф-и т-о по sin (a₀,a_n)=0. 2. если ф-я f(x) задана только на половине промежутка от [0,p] или [-p,0], то можем строить её разложение в ряд Фурье: а) по cos, если периодич. продолжить её четн. образом b) по sin, если периодич. продолжить её нечётн. образом. 3. разложение ф-и на любом отр. T=2l ; ; ; . Пусть задана ф-я y=x построим разложение y=x в ряд Фурье на [-p,p]

Очевидно, что a₀=0, т.е. y=x-нечёт. на [-p,p]. По этой же причине все a_n=0. Вычислим b_n. 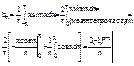В итоге получаем следующее разложение . На (-p,p) ф-я f(x) совпадает с x. . Покажем на графике чему будет равна S₀ в точках разрыва, для этого в этих точках отметим значения S₀=0.