
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Метод максимального правдоподобия. Рассмотрим основные методы получения оценок параметров распределения генеральной совокупности
|
|
Рассмотрим основные методы получения оценок параметров распределения генеральной совокупности.
Этот метод, предложенный Р. Фишером, состоит в следующем. Пусть закон распределения генеральной совокупности X описывается функцией плотности распределения 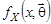 , если X относится к непрерывному типу или вероятностями
, если X относится к непрерывному типу или вероятностями 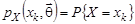 , если X дискретна. Здесь
, если X дискретна. Здесь 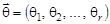 — вектор неизвестных параметров, для которых необходимо получить точечные оценки.
— вектор неизвестных параметров, для которых необходимо получить точечные оценки.
Рассмотрим функцию 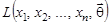 , описывающую закон распределения вектора случайной выборки
, описывающую закон распределения вектора случайной выборки 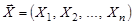 . Она называется функцией правдоподобия. Поскольку случайные величины { Xi } независимы в совокупности, функция правдоподобия имеет вид
. Она называется функцией правдоподобия. Поскольку случайные величины { Xi } независимы в совокупности, функция правдоподобия имеет вид

|
Метод максимального правдоподобия состоит в том, что в качестве оценок параметров 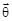 берётся вектор
берётся вектор 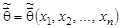 , доставляющий максимум функции правдоподобия при заданных значениях x 1, x 2,..., xn:
, доставляющий максимум функции правдоподобия при заданных значениях x 1, x 2,..., xn:
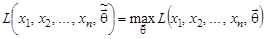
|
Точечные оценки, полученные методом максимального правдоподобия, называют МП-оценками.
При поиске точки максимума 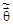 функции
функции 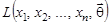 для упрощения расчётов можно:
для упрощения расчётов можно:
а) вместо 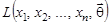 использовать логарифмическую функцию правдоподобия
использовать логарифмическую функцию правдоподобия 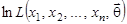 , т.к. от логарифмирования по основанию e > 1 точки максимума не изменяются;
, т.к. от логарифмирования по основанию e > 1 точки максимума не изменяются;
б) не учитывать (отбрасывать) в выражении для функции правдоподобия слагаемые и положительные сомножители, не зависящие от параметров 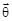 , т.к. и это не изменит точек максимума.
, т.к. и это не изменит точек максимума.
Как правило, МП-оценки получают из необходимого условия экстремума дифференцируемой функции:
| (10.1) | 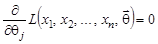 или или 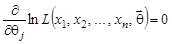
|
| где | j = 1, 2,..., r. |
Уравнения (10.1) называют уравнениями правдоподобия. Для наиболее важных распределений генеральной совокупности уравнения правдоподобия имеют единственное решение 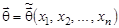 , дающее точечную оценку.
, дающее точечную оценку.
Date: 2015-06-05; view: 642; Нарушение авторских прав