Числовые характеристики выборочного распределения

Рассмотрим выборку (x₁, x₂,..., X_n) как генеральную совокупность 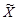дискретного типа со значениями x₁, x₂,..., X_n, которые 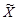принимает с равными вероятностями 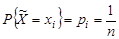, i = 1, 2,..., n.

По определению начальные моменты 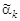и центральные моменты 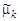такой генеральной совокупности равны, соответственно.

(9.3)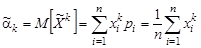
(9.4)	,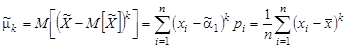
где	.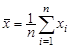

Эти числовые характеристики называются выборочными характеристиками.

Выборочную характеристику

(9.5)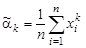

называют выборочным начальным моментом k -го порядка. В частности, момент

(9.6)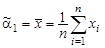

называется выборочным средним.

Выборочная характеристика

(9.7)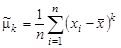

называется выборочным центральным моментом k -го порядка. В частности, при k = 2 получаем выборочную дисперсию

(9.8)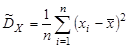

Замечание. При большом объёме выборки (n ³ 50) перечисленные характеристики обычно находят по группированным данным (9.2). Так, если X — генеральная совокупность дискретного типа, то вместо формул (9.6) — (9.8) для подсчёта выборочных моментов 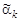и 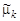используют равенства

(9.9)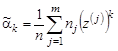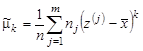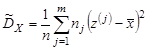

, , , ,

Если же генеральная совокупность X относится к непрерывному типу, то соответствующие равенства выглядят так:

(9.10)	, , , ,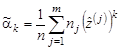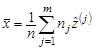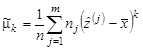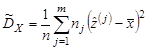
где	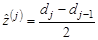— середины промежутков разбиения.

Аналогично вводятся выборочные характеристики многомерных генеральных совокупностей (случайных векторов). Например, пусть (x ₁, y ₁), (x ₂, y ₂),..., (x _n, y _n) — выборка объёма n из двумерной генеральной совокупности (X, Y).

Выборочной ковариацией называют величину

(9.11)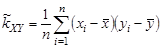

Выборочным коэффициентом корреляции называют величину

(9.12)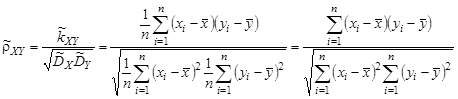

Рассмотрим формулы, упрощающие вычисление выборочных характеристик (9.8) — (9.12).

Date: 2015-06-05; view: 542; Нарушение авторских прав