Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?
Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника
Гистограмма относительных частот
|
|
Графическим представлением статистического ряда (рис. 9.2) является гистограмма — график эмпирической плотности распределения генеральной совокупности непрерывного типа.
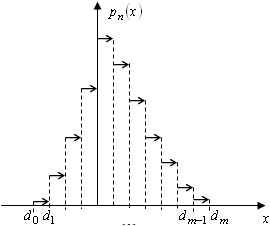
Рис. 9.2. Гистограмма относительных частот
Эмпирической плотностью распределения, соответствующей выборке (x1, x2,..., xn), называется кусочно-постоянная функция
| (9.2) |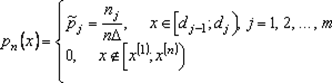 
|
Её график называют гистограммой, на (рис. 9.3).
Часто гистограммой называют диаграмму, составленную из прямоугольников (столбиков) с основаниями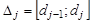 
и высотами 
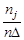, j = 1, 2,..., m. Поскольку 
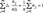, площадь такой диаграммы равна 1. Кроме того, площади прямоугольников равны относительным частотам 
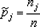попадания элементов выборки в промежутки 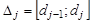статистического ряда (рис 9.3).
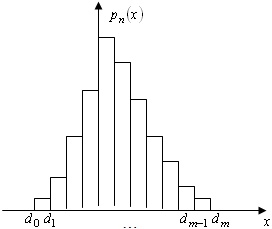
Рис. 9.3. Гистограмма
Наряду с гистограммой используют и другое графическое представление статистического ряда — полигон частот. Это ломанная, звенья которой соединяют середины горизонтальных отрезков, ограничивающих гистограмму сверху (рис. 9.4).
Рис. 9.4. Полигон частот
Полигон частот используют также для представления статистических данных о дискретной генеральной совокупности X. В этом случае на оси абсцисс откладывают значения z (j), полученные в измерениях, и отмечают на координатной плоскости точки (z (j), nj), затем соседние точки соединяют отрезками прямой. Эмпирическую функцию распределения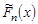 
можно рассматривать как приближённое представление функции распределения 
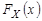генеральной совокупности X, (рис. 9.5). С увеличением объёма выборки n точность и достоверность этого представления возрастают.
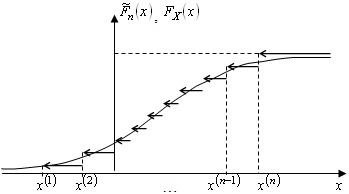
Рис. 9.5. Приближённое представление функции распределения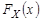 
с помощью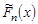
Гистограмма относительных частот pn (x) даёт приближённое представление функции плотности распределения вероятностей fX (x) генеральной совокупности X (рис. 9.6).
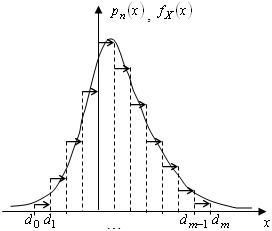
Рис. 9.6. Приближённое представление функции плотности распределения вероятностей
Сказанное выше означает, что предварительная обработка выборки, несмотря на её относительно небольшую трудоёмкость, даёт достаточно полное и наглядное представление о законе распределения генеральной совокупности X.
Date: 2015-06-05; view: 1073; Нарушение авторских прав