Точечные оценки параметров распределения

Одна из задач математической статистики — оценка неизвестных параметров закона распределения генеральной совокупности X. При этом, во многих случаях вид закона распределения X считается известным и задача сводится к нахождению приближённых значений неизвестных параметров этого распределения с использованием выборки из генеральной совокупности.

Пусть 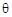— неизвестный параметр распределения, а его приближённое значение находится по выборке (x ₁, x ₂,..., x_n) с помощью функции 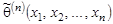элементов выборки: 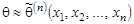. Для выяснения свойств, которыми должна обладать функция 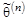, её рассматривают как функцию 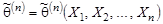случайной выборки (X ₁, X ₂,..., X_n). Любую функцию случайной выборки называют статистикой.

Определение. Точечной оценкой параметра 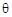распределения генеральной совокупности X называется статистика 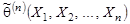, реализации которой 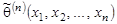используются в качестве приближённых значений этого параметра.

Наряду со статистикой 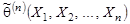, точечной оценкой параметра 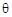мы будем называть и функцию n переменных .

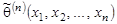Аналогичным образом можно ввести точечные оценки и для вектора неизвестных параметров .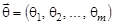

Качество оценки характеризуется основными следующими основными свойствами.

Несмещённость точечной оценки

Статистику 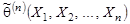называют несмещённой оценкой параметра 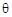, если её математическое ожидание совпадает с 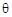для любого фиксированного n:

(9.13)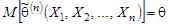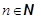

, .

Если же это требование выполняется в пределе, т.е.

(9.14)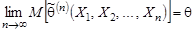

,

то оценку 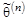называют асимптотически несмещённой.

Несмещённость оценки означает её верность «в среднем», отсутствие систематической ошибки.

Date: 2015-06-05; view: 573; Нарушение авторских прав