Прямая линия на плоскости с прямоугольной системой координат. Нормальное уравнение прямой

Пусть на плоскости задана прямоугольная декартова система координат 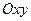, тогда угол между прямыми, определяющийся углом между направляющими векторами может быть определен формулой: .

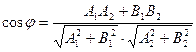Отметим, что угол между прямыми принимает значение от 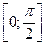, угол между направляющими .

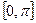Поэтому угол между прямыми определяется углом между векторами. Получаем, что прямые (7), (8) в прямоугольной системе координат ортогональны Û 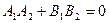(15)

Отметим, что только прямоугольной декартовой системе координат вектор 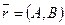является перпендикулярной к прямой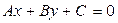

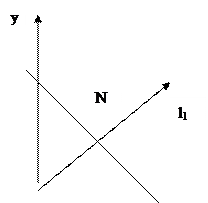
В дальнейшем построим нормальное уравнение на плоскости. В начале введем уравнение прямой в полярной системе координат. Пусть полярная ось совпадает с Ox и l₁ – ось, проходящая через начало координат перпендикулярно прямой l.

			x

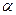
Рис.3.

Пусть прямая 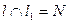и пусть длина

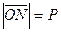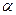, - угол между l₁ и 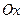. Если т. М лежит на l₁, то очевидно, что проекция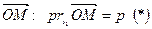

Последнее условие является необходимым и достаточным, для того, чтобы т. М .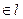

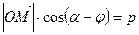или 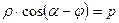, (16)

где 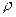- расстояние от т. М до начала координат,

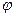- угол между 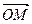и .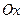

Другими словами, 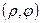- полярные координаты т. М. Таким образом, уравнение (16) является уравнением прямой в полярной системе координат. Уравнение (16) можно переписать: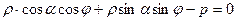

,

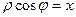
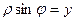где 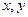- координаты т. М в соответствующей прямоугольной декартовой системе координат.

Получаем: 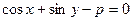(17) – нормальное уравнение прямой на плоскости, где

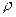- длина перпендикуляра, проведенного из начала координат на прямую,

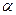- угол наклона нормали к оси абсцисс.

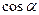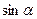Отметим, что и - координаты ортонормали. Покажем, что общее уравнение прямой привели к нормальному виду.

Пусть прямая l: 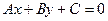, тогда нормальное уравнение получается умножением на некоторый нормирующий множитель 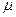: 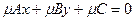при этом 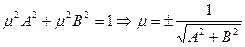, знак 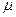выбирается из условия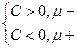

Если С= 0, то знак 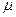произвольный.

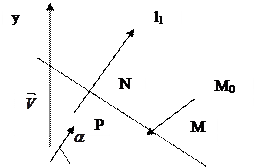
Нормальное уравнение прямой удобно для нахождения расстояния между от произвольной точки плоскости до прямой.

Рис.4.

Произвольная точка .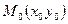

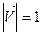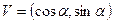, . Очевидно, что расстояние от 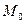до l:

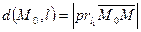
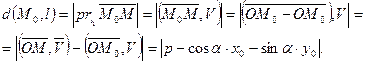
Таким образом, получили, что расстояние от точки до прямой вычисляется следующим образом: в левую часть нормального уравнения этой прямой необходимо подставить координаты т. и полученную величину взять по модулю.

Замечание. Из рисунка видно, что если т. 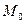и начало координат лежат по разные стороны от l, то 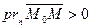. В первом случае: 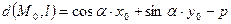, во втором - .

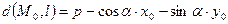Последнее может быть использовано, чтобы узнать лежит ли т. 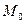и начало координат по одну сторону или по разные от прямой l.

Date: 2015-04-23; view: 676; Нарушение авторских прав