Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?
Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника
Вычисление векторного произведения в прямоугольных координатах
|
|
Пусть задана прямоугольная декартова система координат. Легко видеть, что для базисных векторов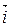 
, 
, 
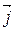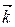справедливо:
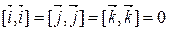Þ очевидно, из коллинеарности.
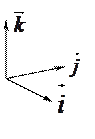
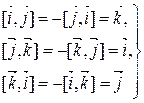. Из этого следует, что 
.
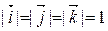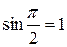(см. рисунок).
Тогда для двух векторов
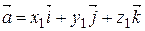и 
.
И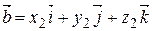меем:
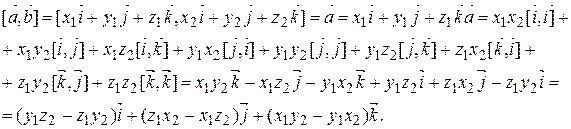
Это равенство формально можно переписать в виде
.
Пример. Вычислить синус угла между векторами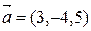 
, 
.
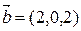Имеем: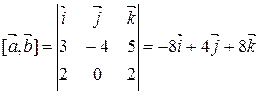 
. 
. 
.
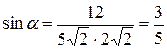Так как модуль векторного произведения численно равен площади параллелограмма, построенного на перемножаемых векторах, то если , .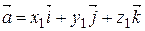
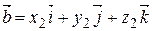Имеем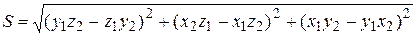 
.
Если параллелограмм расположен в плоскости, то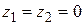 
и 
.
Пример. Даны три точк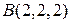и 
, 
и 
.
Найти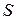 
.
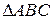Решени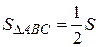е. 
, где 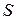– площадь параллелограмма, построенного на векторах 
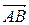и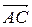 
. Имеем: 
, 
.
.
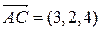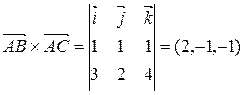
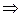
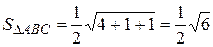6о. Смешанное произведение векторов
Пусть даны три вектора 
, 
, 
.
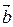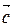Определение 1. Смешанным произведением векторов называется произведение следующего вида: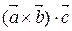 
, т.е. вначале вектора и 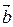перемножаются векторно, а затем результат умножается скалярно на вектор .
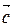В результате получается скалярная величина.
Date: 2015-04-23; view: 479; Нарушение авторских прав