
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Свойства векторного произведения. 1. Векторное произведение двух не нулевых векторов равно нулю Û вектора–сомножители коллинеарны
|
|
1. Векторное произведение двух не нулевых векторов равно нулю Û вектора–сомножители коллинеарны.
Доказательство:
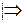 Пусть
Пусть 
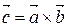 и
и 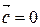 Þ
Þ 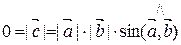 Þ т.к.
Þ т.к. 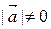 ,
, 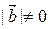 Þ
Þ 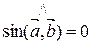 Þ
Þ 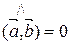 , т.е.
, т.е.  ||
|| 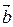 .
.
 Пусть
Пусть  ||
|| 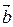 , тогда
, тогда 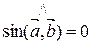 Þ
Þ 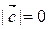 Þ
Þ 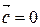 .
.
2. Длина векторного произведения численно равна площади параллелограмма, построенного на перемножаемых векторах.
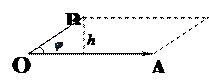 Доказательство:
Доказательство:
Пусть 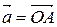 и
и 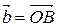 . На отрезках [OA] и [OB] построим параллелограмм.
. На отрезках [OA] и [OB] построим параллелограмм.
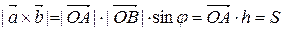 .
.
3. Векторное произведение антикоммутативно, т.е. 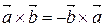 .
.
Доказательство:
Легко видеть, что 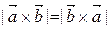 , т.к. вектора
, т.к. вектора  ,
, 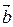 ,
, 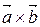 образуют правую тройку, то тройка
образуют правую тройку, то тройка 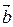 ,
,  ,
, 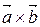 – левая Þ т.е. вектора
– левая Þ т.е. вектора 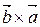 и
и 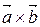 – противоположно направлены. Следовательно,
– противоположно направлены. Следовательно, 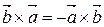 .
.
4. 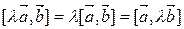 .
.
Докажем первое равенство.
1) В начале покажем равенство модулей.
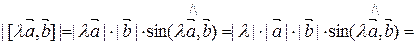
т.к. 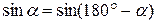 , то
, то 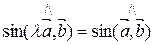 .
.
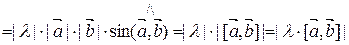 .
.
2) Так как 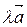 ||
||  , то
, то 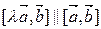
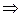
 .
.
5. Покажем, что 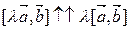 . Рассмотрим случай
. Рассмотрим случай 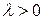 и
и 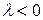 .
.
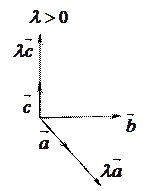
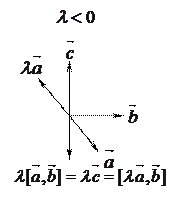
Отсюда вытекает доказываемое свойство.
6. 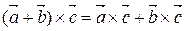 – дистрибутивность.
– дистрибутивность.
Если один из векторов нулевой – очевидно. Пусть  ,
, 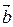 ,
, 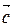 – не нулевые. Для доказательства воспользуемся описанным ранее методом построения векторного произведения.
– не нулевые. Для доказательства воспользуемся описанным ранее методом построения векторного произведения.
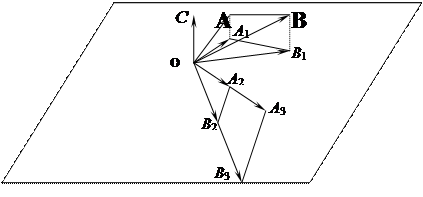 |
Выберем произвольную точку 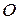 и отложим из нее вектора
и отложим из нее вектора  и
и 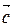 . Из конца вектора
. Из конца вектора  построим вектор
построим вектор 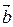 . Т.о.,
. Т.о., 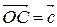 ,
, 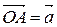 ,
, 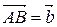 ,
, 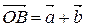 .
.
1) Построим плоскость П^ 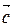 .
.
2) Спроецируем 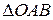 на плоскость П: получим
на плоскость П: получим 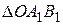 .
.
3) Повернем 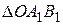 по часовой стрелке на угол p¤2.
по часовой стрелке на угол p¤2.
4) Умножим отрезки сторон на 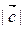 , получим треугольник
, получим треугольник 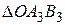 подобный
подобный 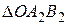 .
.
По построению, 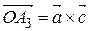 ,
, 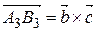 ,
, 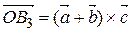 Þ т.к.
Þ т.к. 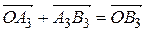 ), то
), то 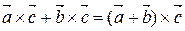 .
.
Date: 2015-04-23; view: 733; Нарушение авторских прав