Векторное, параметрическое, общее и каноническое уравнение прямой

Зафиксируем на плоскости аффинную систему координат, определяемую точкой О - началом координат, базисным вектором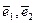

Тогда " точка плоскости 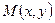определяется координатами .

Зафиксируем на плоскости некоторую прямую линию.

Определение 1. Всякий ненулевойвектор 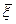∥ прямой l называется направляющим вектором этой прямой.

Пусть есть точка 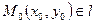, тогда производная точки 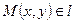лишь при условии, когда вектор 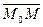коллинеарен .

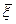Другими словами это означает, что 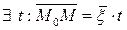(1)

С другой стороны всякая точка М, для которой выполнено уравнение (1) принадлежит прямой в силу определения произведения вектора на число.

Таким образом т. М 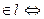выполняется (1). Уравнение (1) называется векторным уравнением прямой.

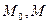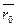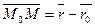Если обозначить радиус вектора т. через и соответственно, то и уравнение (1): 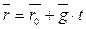, (2)

также называется векторным уравнением прямой.

Если 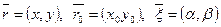, то (2) в координатах:

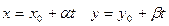(3)

- параметрическое уравнение прямой на плоскости, проходящей через т. 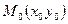в направлении .

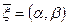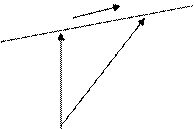Рис.1

Исключая из уравнения (3) параметр t получаем 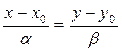(4)

- каноническое уравнение прямой на плоскости.

Уравнение (4) необходимо воспринимать, как пропорцию, если 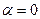, то это прямая ∥-ая оси Oy, проходящей через т. .

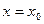Приведем уравнение (4) к общему знаменателю: 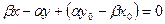. Если обозначить 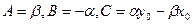получаем: 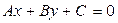(5)

- общее уравнение прямой на плоскости.

Так как 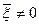, то один из коэффициентов А или В отличен от нуля ⇒ уравнение (5) представляет собой уравнение первого порядка.

Показали, что " прямая является алгебраической линией первого порядка.

Покажем, что " алгебраическая линия первого порядка на плоскости является прямой.

Действительно, уравнение (5) имеет частное решение, например:

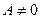, то можно выбрать 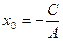, , 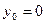тогда полученное решение можно???, как координаты точки 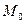, через которую проходит искомая прямая.

В качестве 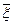прямой K вектор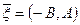

Покажем, что т. 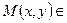прямой лишь при условии, когда её координаты удовлетворяют уравнению (5).

Действительно, по построению 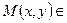прямой, если 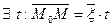, т.е.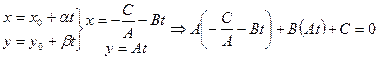

0=0 получаем тождество

Таким образом доказана следующая теорема:

Теорема 1. Прямые на плоскости – алгебраические линии первого порядка.

Из доказательства теоремы 1 следует, что если 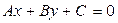- уравнение прямой, то вектор 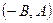является направляющим вектором этой прямой.

Рис.2.

Если , то из уравнения (5) получаем: 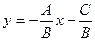, т.е. , где .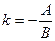

.

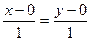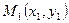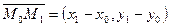Вместе с каноническим уравнением (4) используется уравнение прямой, проходящей через 2 точки: если l проходит через точку и , то можно выбрать K в качестве направляющего вектора прямой, поэтому уравнение 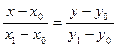(6)

называется уравнением прямой, проходящей через т. 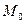и .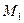

??? частные случаи уравнения (5):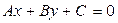

1. А=0 прямая ∥-ая Ox

2. B=0 прямая ∥-ая Oy

3. C=0 проходящая через начало координат

4. A=C=0 ось Ox

5. B=C=0 ось Oy

Date: 2015-04-23; view: 778; Нарушение авторских прав