Взаимное расположение прямых на плоскости. Полуплоскости

Пусть на плоскости задана аффинновая система координат .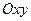

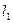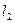Утверждение 1. Для того, чтобы прямые и , заданные уравнениями 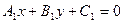(7)

(8)

соответственно совпадали необходимо и достаточно, чтобы 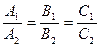(9)

|Þ 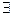l₁ и l₂ совпадают, это означает, что их направляющие вектора 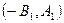и 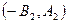коллинеарные, т.е. 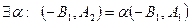(10)

Возьмем т. 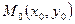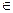этим прямым, тогда ,

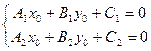Умножая первое уравнение на 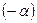и прибавляя по??? в силу (10): 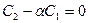(11)

Формулы (10), (11) эквивалентны (9)

Ü| пусть выполняется (9), тогда уравнения (7) и (8) эквивалентны Þ соответствующие прямые совпадают, ч.т.д.∎

Утверждение 2. Прямые 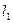и 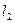, заданные уравнениями 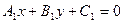, параллельны и не совпадают Û 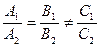(12)

Доказательство.

|Þ прямые параллельны и не совпадают Þ 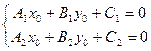несовместна, а это возможно, по теореме Кронекера-Конелли Û ,

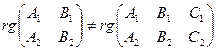возможно лишь при условии 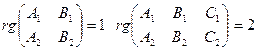это возможно при выполнении (12)

Ü| Если выполняется первое равенство Þ прямые параллельны, а не выполнение второго Þ система (7), (8) несовместна Þ прямые параллельны и не совпадают, ч.т.д.∎

Следствие (из 1,2). Прямые 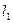и 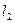пересекаются Û 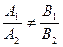(13)

Утверждение 3. Пусть прямые 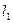и 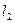, задаваемые уравнениями (7,8), пересекаются в единственной точке с координатами 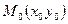, тогда прямая l₃ проходит через т. 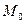Û она задается уравнением: 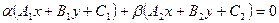(14)

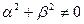
Т.е. уравнение (14) – линейная комбинация (7,8)

Доказательство.

|Þ Очевидно, а именно, если уравнение l₃ задается (14), то она проходит через т.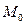

Ü| пусть l₃ проходит через т. 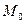и имеет уравнение .

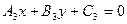Возьмем на прямой l₃ " т. 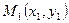, отличную от т. 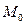. Выберем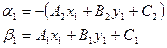

Покажем, что уравнение для l₃ пропорционально (14) с выбранными .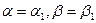

Т.к. т. 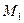не может одновременно принадлежать прямым 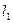и 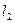и Þ хотя бы одно из 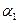и 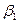отлично от нуля. Поэтому уравнение 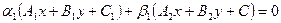является уравнением первой степени Þ определяет некоторую прямую.

По построению эта прямая проходит через т. 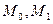, т.к. через две точки плоскости, то она совпадает с прямой 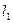. Поэтому в силу утверждения 1, уравнения этих прямых пропорциональны, ч.т.д.∎

Уравнение (14) называется уравнением пучка прямых, проходящих через т. .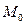

Date: 2015-04-23; view: 532; Нарушение авторских прав