Как пример линейного пространства

1^о. Направленные отрезки.

Рассмотрим в пространстве две точки А и В. Они определяют отрезок АВ.

Определение 1. Отрезок АВ называется направленным, если его концы А и В упорядочены; если при этом первой является точка А, а второй – точка В, то А – начало отрезка, а В – его конец.

Направленный отрезок обозначается 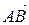или 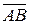. На чертеже направленный отрезок снабжен стрелкой на конце(см. рис.1)

Определение 2. Длиной 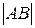направленного отрезка 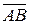называется длина отрезка АВ.

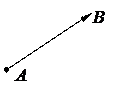Рис.1. Направленный отрезок АВ.

Определение 3. Направленные отрезк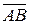и и 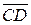называются сонаправленными (обозначается 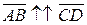), если они лежат на параллельных прямых и направлены в одну сторону.

Направленные отрезк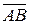и и 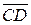называют противоположно направленными (пишут 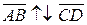), если они лежат на параллельных прямых и направлены в разные стороны.

Направленные отрезк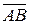и и 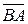называются противоположными.

Каждую точку А пространства можно рассматривать как направленный отрезок с совпадающим началом и концом. Этот отрезок обозначается 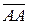и называется нулевым направленным отрезком. Его длина считается равной нулю, а направление не определено.

Определение 4. Два направленных отрезка 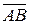и 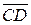считаются эквивалентными, если они сонаправлены и имеют равные длины. (Обозначают ).

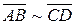Эквивалентность является отношением эквивалентности в множестве всех направленных отрезков, т.к. из определения эквивалентности следует:

1) отрезок 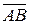эквивалентен сам себе;

2) если 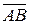эквивалентен 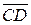, то 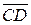эквивалентен ;

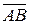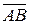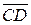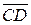3) если эквивалентен и эквивалентен 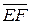, то 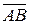эквивалентен .

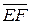Так как эквивалентность направленных отрезков является отношением эквивалентности, то множество всех направленных отрезков пространства разбивается на непересекающиеся классы – классы эквивалентности. Классы эквивалентности образуют фактор-множество множества всех направленных отрезков пространства.

Определение 5. Множество всех эквивалентных направленных отрезков называется вектором (или свободным вектором).

Замечание. Напомним, что в средней школе вектор характеризуетпараллельный перенос.

Направление эквивалентных направленных отрезков называется направлением вектора, а их длина – длиной вектора.

Таким образом, любой направленный отрезок однозначно определяет вектор, а вектор – это класс эквивалентных направленных отрезков.

Поэтому часто будем пишут вектор , .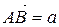

Определение 6. Вектор a такой, что 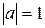называется единичным вектором или ортом. Множество нулевых отрезков называется нулевым вектором 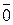; Его длина равна нулю, а направление не определено.

Определение 7. Два ненулевых вектора, направления которых совпадают или противоположны, называются коллинеарными. Обозначают .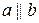

Нулевой вектор считается коллинеарным любому вектору.

Очевидно, что прямые, на которых лежат представители классов коллинеарных векторов, параллельны.

Определение 8. Три и более векторов называются компланарными, если они параллельны некоторой плоскости.

Для определенности любую тройку векторов, содержащую нулевой вектор, считают комплонарной.

Пусть даны два вектора a и b. Из произвольной точки O пространства отложим 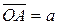и 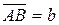. Тогда 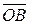есть направленный отрезок и значит, определяет вектор.

Покажем, что вектор 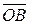не зависит от выбора точки O. Для этого выберем другую точку 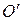. Пусть 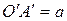, 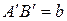. Тогда 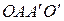– параллелограмм; аналогично, 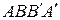– параллелограмм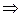 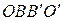– параллелограмм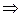 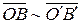, т.е. они определяют один и тот же вектор.

Определение 9. Вектор 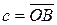называется суммой векторов 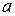и 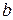. Пишут: .

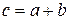Способ сложения векторов, изложенный выше, называется правилом треугольника. Можно также использовать правило параллелограмма.

Date: 2015-04-23; view: 429; Нарушение авторских прав