Доказательство

1. Аналогично доказательству из §8.

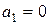
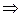
2. Есл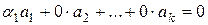и и 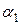– любое, например,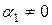 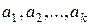линейно зависимы.

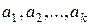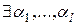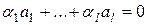
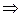
3. Если – линейно зависимы, то одновременно неравные нулю, так что 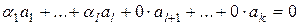и хотя бы одно из 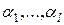отлично от нуля 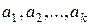линейно зависимы. ч.т.д.

Пример. Рассмотрим линейное пространства 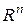и докажем, что n элементов из 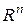вида 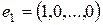, ,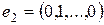…, 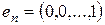линейно независимы, а добавление еще одного элемента 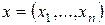приводит к линейно зависимой системе. Действительно, рассмотрим линейную комбинацию 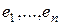с 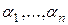. Имеем 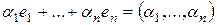. Вектор справа равен нулю, если все 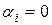, т.е. 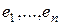– линейно независимы.

Добавим 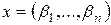. Тогда по теореме 1, п. 1, достаточно показать, что x – линейная комбинация 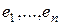. Действительно, .

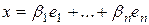3^о. Базис линейного пространства и координаты вектора в базисе.

Определение 5. Совокупность векторов 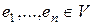называют базисом в 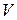, если

1. вектора 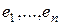– линейно независимы;

2. для 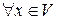найдутся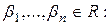 . (1)

При этом равенство (1) называется разложением элемента 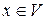по базису 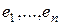, а 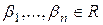называются координатами 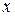относительно базиса .

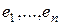Теорема 2 (о единственности разложения по базису). Любой элемент 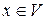может быть единственным образом разложен по базису 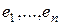, т.е. координаты вектора относительно базиса определяются однозначно.

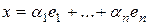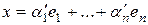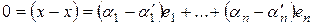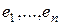
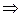
Доказательство. Пусть и . Тогда . В силу линейной независимости 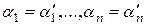, что и требовалось доказать.

Теорема 3 (операции над векторами, заданными своими координатами). При сложении любых двух векторов 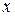и 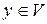их координаты (относительно любого фиксированного базиса в 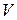) складываются; при умножении 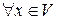на 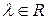, все координаты вектора умножаются на это число.

Доказательство. Пусть 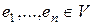– базис в 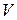, , 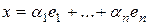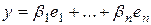. Тогда в силу аксиом линейного пространства 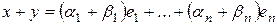, 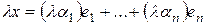. В силу единственности разложения по базису 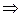что теорема доказана.

Примеры.

1. Базис в 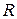– любое ненулевое число.

2. 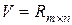. Базис образуют матрицы 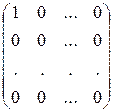, , 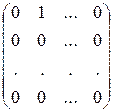…, 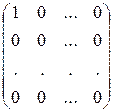с одним единичным элементом.

3. 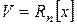– множество многочленов степени не выше n. Базис: , , …, .

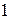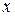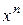4. 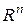– см. выше.

4^о. Размерность линейного пространства.

Определение 6. Линейное пространство 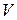называется n–мерным, если

1. В нем 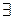n линейно независимых векторов.

2. 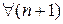векторов линейно зависимы.

Тогда n называется размерностью 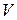и обозначается .

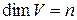Определение 7. Линейное пространство называется бесконечномерным, если в нем 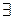любое число линейно независимых векторов.

Выясним связь между понятием базиса и размерности линейного пространства.

Теорема 4. Если 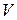– линейное пространство размерности n, то 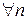линейно независимых векторов этого пространства образуют его базис.

Доказательство. Пусть 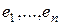– система n линейно независимых векторов из 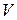. Если 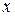– любой вектор из 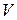, то по Def 6, вектора 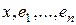– линейно зависимы, т.е.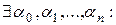

и среди 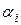есть хотя бы одно отличное от нуля. Очевидно, что 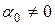(т. к. иначе 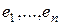– линейно зависимы)

, т.е.

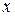– линейная комбинация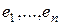 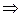т. к. 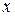– произвольный, то 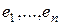–базис.

Теорема 5. Если 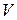имеет базис, состоящий из n элементов, то .

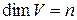Доказательство. Пусть 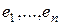– базис в 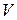. Достаточно показать, что 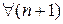векторов 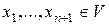линейно зависимы. Разложим их по базису:

,

…

,

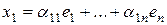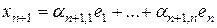где .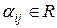

Очевидно, что линейная зависимость векторов 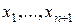эквивалентна линейной зависимости строк матрицы

.

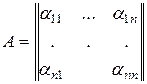Но строки этой матрицы заведомо линейно зависимы, т. к. порядок базисного минора не превосходит n и хотя бы одна из 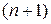строк не является базисной, и по теореме о базисном миноре представляет собой линейную комбинацию базисных строк (а стало быть и остальных).

Примеры.

1. .

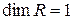2. .

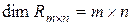3. .

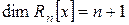4. .

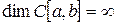5. .

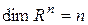5^о. Изоморфизм линейных пространств.

Здесь будет показано, что линейные пространства одной и той же размерности в смысле некоторых свойств, связанных с введенными операциями, не отличаются друг от друга.

Определение 6. Два произвольных линейных пространства V и 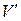над одним и тем же полем 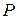называются изоморфными, если между элементами этих пространств можно установить взаимнооднозначное соответствие так, что если векторам 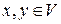отвечают соответственные вектора 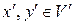, то вектору 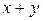отвечает вектор 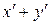, а вектору 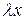при 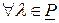отвечает вектор .

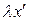Date: 2015-04-23; view: 935; Нарушение авторских прав