Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?
Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника
Примеры. Замечание. Так как − абелева группа, то существует единственный нейтральный (нулевой) элемент
|
|
Обозначение..
Замечание. Так как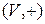 
− абелева группа, то существует единственный нейтральный (нулевой) элемент, обозначаемый 
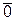, для каждого вектора 
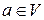существует единственный симметричный (противоположенный) элемент, обозначаемый 
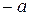, и для 
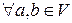уравнение 
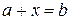имеет единственное решение 
, называемое разностью 
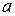и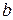 
.
Свойства линейного пространства.
1) 
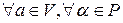выполняется 
.
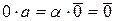2) 
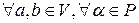выполняется 
.
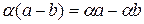3) 
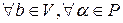выполняется 
.
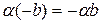4) 
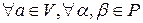выполняется 
.
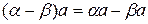5) 
.
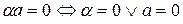6) 
.
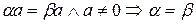7) 
.
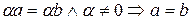Доказательство.
1) Так как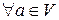 
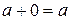
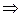в силу г) 
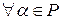имеем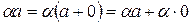 
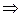
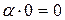. Аналогично, 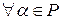имеем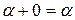 
.
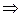
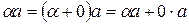
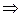
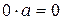2) В силу г) имеем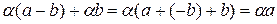 
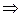в силу разности векторов 
.
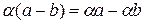3) Следует из 2) при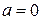 
.
4) Доказывается аналогично.
5) Есл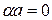и 
и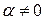 
, то умножая это равенство на 
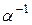получаем: 
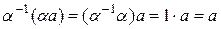и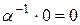 
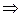
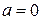. Т.о., если 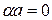, то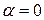 
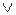
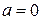. Обратное утверждение следует из 1).
6) Из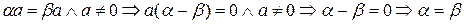 
.
7) Аналогично. ■
Примеры.
1) Если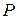 
− поле и 
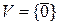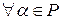, то имеем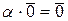 
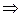
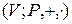− векторное пространство, называемое нулевым.
2) 
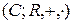− векторное пространство комплексных чисел над полем вещественных чисел. 
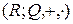− векторное пространство вещественных чисел над полем рациональных чисел.
3) Множество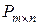 
матриц размера 
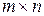образует векторное пространство 
.
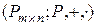4) Множество многочленов степени не выше n образует векторное пространство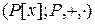 
.
5) Множество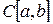 
непрерывных на 
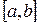функций образует векторное пространство 
.
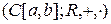6) 
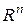– n -мерное координатное пространство (или арифметическое пространство), элементами которого являются упорядоченные наборы из n чисел: 
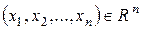. Операции определены следующим образом:
;
.
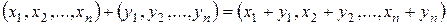Задача. Проверить выполнение аксиом векторного пространства.
2о. Линейно зависимые и линейно независимые системы векторов
Это понятие является обобщением понятия линейной зависимости строк.
Определение 2. Линейной комбинацией векторов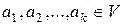 
с коэффициентами 
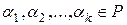называется выражение вида: 
.
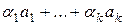Определение 3. Вектора 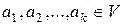называются линейно независимыми, если 
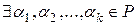, из которых хотя бы одно отлично от нуля, т.е. линейная комбинация 
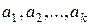с этими 
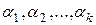является нулевым вектором V, т.е. 
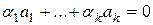. Вектора 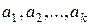, не являющиеся линейно зависимыми, называются линейно независимыми. Другими словами, 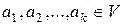называются линейно независимыми, если их линейная комбинация является нулевым элементом V лишь при условии, что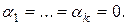 
Date: 2015-04-23; view: 475; Нарушение авторских прав