Вариационно-разностный метод в расчетах балок

Здесь используются экстремальные свойства полной потенциальной
энергии системы, а точнее, принцип возможных перемещений по отношению
к энергии системы, который гласит:

! Для системы, находящейся в равновесии, из всех возможных перемещений, удовлетворяющих заданным граничным условиям, в действительности имеют место те, при которых полная потенциальная энергия принимает минимальное значение.

Полная потенциальная энергия системы состоит из энергии ее деформирования 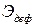и изменения в процессе деформирования потенциала внешней нагрузки :

,

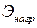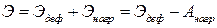где изменение потенциальной энергии нагрузки 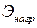равно с обратным знаком работе нагрузки: .

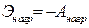Полная потенциальная энергия систем выражается через перемещения (прогибы) и нагрузки. Функция прогибов входит в выражение энергии в виде непосредственно функции y и ее второй производной. Соответственно выражение полной потенциальной энергии системы можно представить в виде:

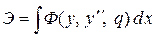. (8.15)

Несложно заметить, что это выражение является функционалом.

Функционал – это функция, которая зависит от одной, либо нескольких функций, и в которой аргумент x в явном виде не присутствует.

Если для обыкновенной функции 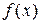значения функции определяются множеством значений аргумента x, то для функционала 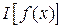его значения определяются множеством функций, подчиняющихся определенным (граничным и другим) условиям.

Определение функции 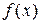, при которой функционал 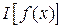, выраженный с помощью определенного интеграла, получает экстремальное значение, является вариационной задачей.

В рассматриваемых задачах мы ищем функцию прогибов (перемещений), которая соответствует минимальному значению энергии.

Функция, которая удовлетворяет такому условию, называется экстремалью, то есть экстремаль – это решение вариационной задачи.

При использовании конечных разностей мы определяем, как уже указывалось, не саму функцию, а ее значения в ряде точек.

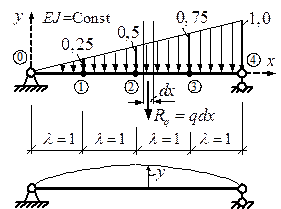Функционал полной потенциальной энергии представляется в конечно-разностной форме, и берутся производные по параметрам перемещений в точках,
которые на основе принципа возможных перемещений приравниваются к нулю:

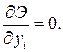(8.16)

Получаем опять систему алгебраических уравнений, решая которую находим перемещения точек.

Рисунок 8.7 Рассмотрим применение вариационно-разностного метода на примере той же балки (рис. 8.7).

Полная потенциальная энергия балки запишется в виде:

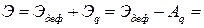
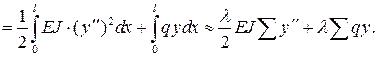
Разбивая балку на четыре участка (рис. 8.7) и учитывая зависимость (8.2) для второй производной, получим:

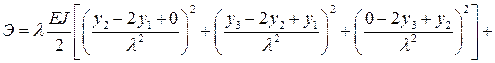
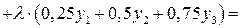
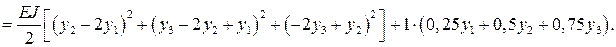
Применяем теперь к полной потенциальной энергии балки условие ее
экстремальности (8.16) и получаем для каждой из узловых точек уравнения:

; ;

; ;

; .

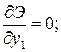
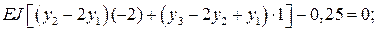
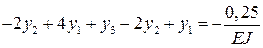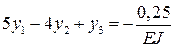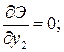
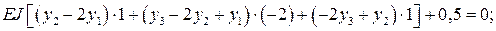
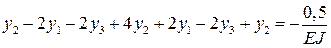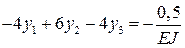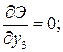
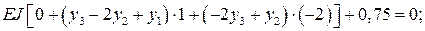
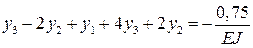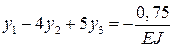Получаем систему трех уравнений, которая полностью совпадает с системой уравнений, полученной при решении дифференциального уравнения
четвертого порядка (8.13).

Достоинством вариационно-разностного метода является то, что функционал энергии содержит производные только второго порядка.

Date: 2015-05-22; view: 1168; Нарушение авторских прав