Матричная форма определения перемещений в рамно-блочных системах

Матричная форма вычислений очень удобна для компьютерных вычислений и программирования. И имеются методы расчета, которые полностью формулируются в матричной форме (например, метод конечных элементов (МКЭ)).

Определение перемещений в стержневых системах может быть выполнено по формуле Мора, имеющей вид:

,

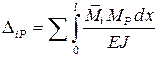где: 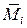– усилия (эпюра усилий) в системе, возникающие от действия единичной «силы», приложенной в точке (в сечении), для которой определяется перемещение, в направлении искомого перемещения; М_Р – усилия (эпюра усилий)
в системе от внешней нагрузки, от действия которой ищется перемещение;
EJ – изгибные жесткости участков системы, в пределах которых эпюры усилий 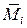и М_Р изменяются непрерывно.

При действии на сооружение сосредоточенных и равномерно распределенных нагрузок возможно, как известно, два случая изменения эпюр усилий 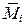и М_Р в пределах участков их одновременной непрерывности, которые могут быть представлены в матричной форме в трех вариантах:

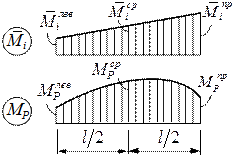
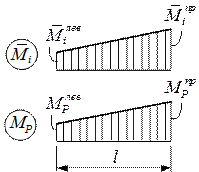1) обе эпюры усилий линейны (рис. 7.1):

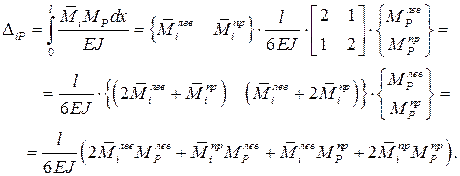Рисунок 7.1

Последнее выражение представляет собой формулу трапеций, поэтому данная матричная форма записи вычисления справедлива, и сокращенно для произвольного k-го участка может быть представлена в виде:

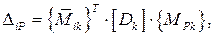(7.1)

где 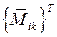– транспонированная матрица ординат из единичной эпюры ;

– вектор (матрица-столбец) ординат на участке из грузовой эпюры M_P;

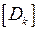– матрица упругой податливости стержня, имеющая в рассматриваемом случае двух линейных на участке эпюр вид:

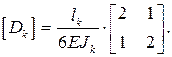(7.2)

2) одна из эпюр усилий (единичная )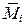
линейна, а вторая (грузовая M_P) – изменяется
по параболической зависимости, при записи
на обеих эпюрах трех ординат (в начале, в середине и в конце участка) (рис. 7.2):

Рисунок 7.2

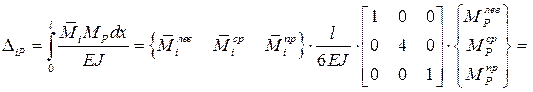
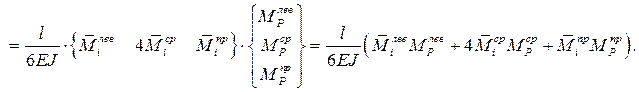
Последнее выражение представляет собой формулу Симпсона.

Сокращенно матричная форма вычисления интеграла Мора для произвольного (k-го) участка может быть записана так же, как и в первом случае (7.1), но здесь матрица упругой податливости стержня на участке имеет другой вид:

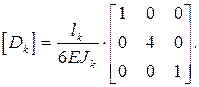(7.3)

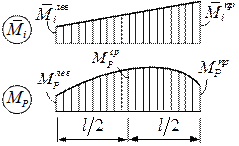
3) одна из эпюр усилий (единичная 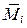) линейна, а вторая (грузовая M_P) – изменяется по параболической зависимости, при записи для линейной эпюры двух ординат (в начале и в конце участка), для параболической эпюры – трех ординат (в начале, в середине и в конце участка) (рис. 7.3):

22.

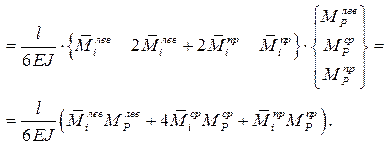
23.

Рисунок 7.3

24.

Последнее выражение также представляет собой формулу Симпсона.

Сокращенно матричная форма записи вычисления для произвольного k-го участка может быть записана так же, как в первом и втором случаях (7.1), но здесь матрица упругой податливости стержня на участке имеет другой вид:

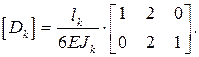(7.4)

Расчетные системы сооружений обычно имеют не один участок, а разделяются на целый ряд участков, по которым следует суммировать «перемножение» эпюр. В результате матричная форма определения перемещений может быть представлена в виде:

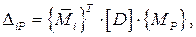(7.5)

где: 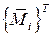– транспонированная матрица ординат из единичной эпюры 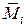(ор-

динаты записываются последовательно для всех участков в соответствии
с ранее рассмотренными принципами в строку); – вектор (матрица-столбец) ординат из грузовой эпюры M_P, записываемых по участкам в столбец;

– квазидиагональная матрица упругой податливости системы, имеющая вид:

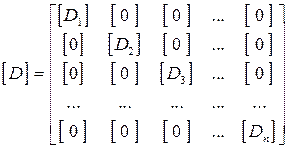, (7.6)

где: n– число участков одновременной непрерывности эпюр в системе;

– матрицы жесткости отдельных участков, вид которых определяется выражениями (7.2) – (7.4);

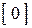– нулевые матрицы, все элементы которых равны нулю.

Матричная форма позволяет определять сразу несколько (m) перемещений от действия нескольких (s) нагрузок, и тогда выражение для определения перемещений принимает вид:

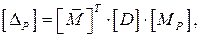(7.7)

где: 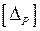– матрица перемещений:

; (7.8)

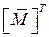– транспонированная матрица ординат из единичных эпюр, состоящая из m строк, в которые записываются ординаты по участкам из единичных эпюр 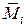(i = 1 … m):

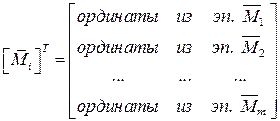; (7.9)

– матрица, состоящая из s столбцов ординат по участкам из грузовых эпюр M_P (число столбцов равно количеству вариантов нагрузок, от действия которых определяются перемещения):

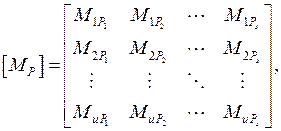(7.10)

где u – число сечений, в которых записываются ординаты усилий.

Матрица упругой податливости [D] в (7.7) имеет тот же вид (7.6).

Date: 2015-05-22; view: 1234; Нарушение авторских прав