Нелинейные уравнения и методы их решения

Нелинейными называют уравнения , в которых функция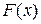
зависит от аргумента х нелинейно.

Нелинейные уравнения разделяют на алгебраические и трансцендентные. Алгебраическими являются уравнения, содержащие только алгебраические функции (степенные, рациональные, иррациональные). Трансцендентные уравнения содержат тригонометрические, показательные, логарифмические и другие подобные функции.

Методы решения нелинейных уравнений делятся на прямые и итерационные.

Прямые методы позволяют записать решение в виде некоторого конечного соотношения (формулы). Вспомним, например, решение квадратного уравнения, некоторых тригонометрических и показательных уравнений.

Нелинейные уравнения, получаемые при расчете сооружений, чаще всего решить такими простыми методами не удается, и приходится использовать
итерационные методы – методы последовательных приближений.

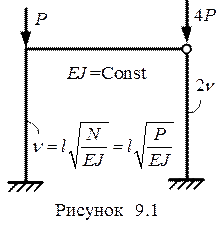Нелинейные уравнения получаются, например, при решении задач устойчивости. Так при расчете на устойчивость рамы, представленной на рис. 9.1, уравнение для нахождения критической нагрузки (критического параметра устойчивости v, через который выражается критическая нагрузка – ) в общем случае может иметь вид:

или 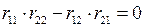, (9.1)

где величины 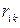выражаются через функции

, которые являются трансцендентными и имеют достаточно сложные зависимости, например, вида:

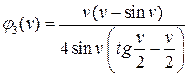; , где ,

а N – величина продольной силы в сжатом стержне в недеформированном
состоянии.

Уравнение устойчивости (9.1) для рамы на рис. 9.1 может иметь вид:

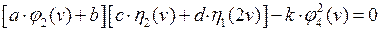, (9.2)

где значения коэффициентов а, b, c, d, k в уравнении зависят от размеров рамы и соотношений жесткостей ее стержней.

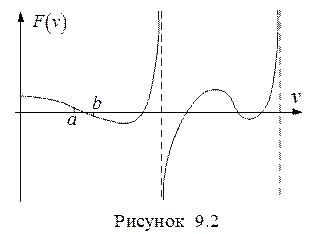
Уравнение (9.2) является нелинейным и его левая часть может иметь вид, показанный, например, на рис. 9.2.

Для решения подобных нелинейных уравнений чаще всего используют итерационные методы, алгоритм нахождения решения которыми состоит обычно из двух этапов:

1) отыскание приближенного значения решения или содержащего его отрезка;

2) уточнение решения до некоторой заданной точности непосредственно итерационным методом.

Первый этап решения заключается в нахождении отрезка 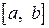, в пределах которого будет находиться решение. В точках а и b функция 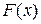должна принимать значения разных знаков (рис. 9.2), то есть должно выполняться условие:

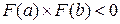. (9.3)

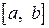В этом случае между точками а и b будет, по крайней мере, одна точка, в которой функция будет равна нулю (). Отыскание отрезка необходимо начинать с начала изменения функции и, задавая достаточно малый шаг
изменения аргумента , чтобы случайно не проскочить первое решение, необходимо последовательно вычислять значения функции в очередных точках, проверяя выполнение условия (9.3).

После нахождения отрезка , содержащего решение, необходимо уточнять решение. Каждый шаг уточнения называется итерацией. В результате получим последовательность приближенных значений решения: . Если эти значения постепенно приближаются к истинному значению, то говорят, что итерационный процесс сходится, и наоборот.

Date: 2015-05-22; view: 839; Нарушение авторских прав