Формула Симпсона

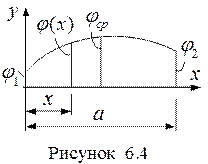
Параболическая функция. При рассмотрении вопросов аппроксимации (раздел 5) для параболической функции (рис. 6.4) получено выражение в виде:

.

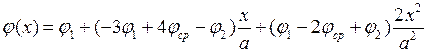Подставим это выражение в интеграл и выполним интегрирование:

=

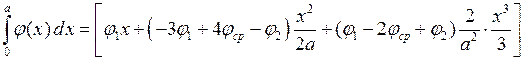
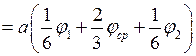
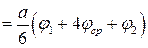. (6.4)

Получили выражение, которое называют
формулой Симпсона для вычисления интегралов, содержащих одну параболическую функцию одной переменной.

Формула Симпсона. Рассмотрим интеграл вида (6.5) от двух функций, где
одна из функций 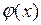будет изменяться по параболической зависимости, а вторая 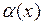будет линейной (рис. 6.8):

;

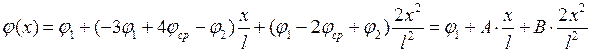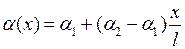, (6.7)

где: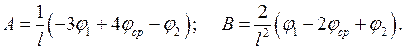

Подставляем зависимости (6.7) в (6.5) и выполняем интегрирование:

=

= = =

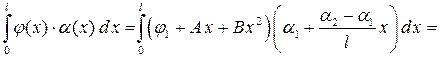
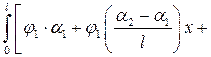
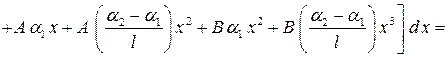
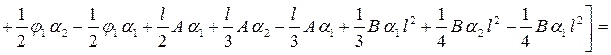
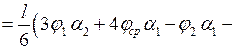
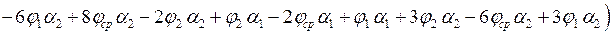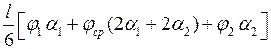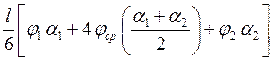= (6.8)

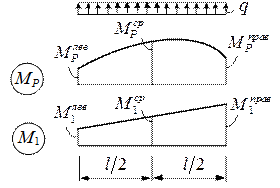
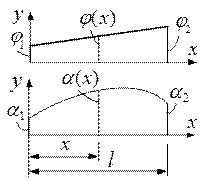
Рисунок 6.8 Рисунок 6.9

Получаем выражение, которое называют формулой Симпсона.

Для функций в виде изгибающих моментов (рис. 6.9) формула Симпсона будет иметь вид:

. (6.8ˊ)

Полученные формулы для численного интегрирования (6.6) и (6.8) позволяют вычислять перемещения как в рамно-балочных, так и в арочных и комбинированных системах. При этом для рам и балок, для которых зависимости
изменения эпюр усилий являются линейными и параболическими, данные формулы будут давать точный результат, а для арок – будем получать приближенные значения.

Date: 2015-05-22; view: 1050; Нарушение авторских прав