Определение перемещений в арочных системах

Определение перемещений в трехшарнирных арках выполняется по формуле Мора:

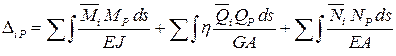, (6.9)

где: 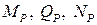– зависимости изменения изгибающих моментов, поперечных и продольных сил от внешней нагрузки, от действия которой определяется перемещение; 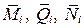– зависимости изменения усилий от единичной нагрузки, приложенной в точке (в сечении), в которой определяется перемещение в направлении искомого перемещения; 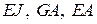– зависимости изменения изгибной, сдвиговой и продольной жесткостей арки; η – коэффициент, учитывающий неравномерность распределения касательных напряжений при изгибе (для прямоугольного сечения он равен 1,2); d s – элементарная длина дуги арки, выражаемая через бесконечно малое горизонтальное расстояние d х зависимостью 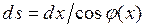(рис. 6.10).

Усилия в сечениях трехшарнирных арок определяются зависимостями:

;

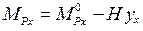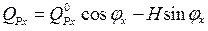; (6.10)

,

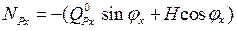де: 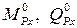– изгибающие моменты и поперечные силы в сечении х
двухопорной балки, имеющей такой же пролет, как арка, и загруженной такой же нагрузкой; Н – распор в арке; φ_х – угол наклона касательной к оси арки в
сечении х по отношению к горизонтальной оси.

Зависимости (6.10) представляют собой сложные нелинейные функции, и при подстановке их в (6.9) непосредственное интегрирование выражений является часто очень непростой задачей. Поэтому вычисление интегралов здесь
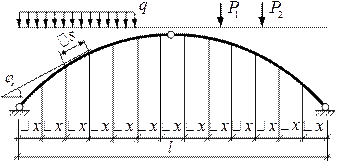
чаще всего выполняют численно, разбивая пролет арки на определенное число малых частей Δ х (рис. 6.10).

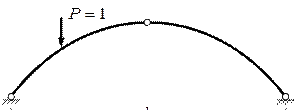Таким образом, для определения перемещений необходимо построить эпюры усилий от действия внешней нагрузки (6.10) и от действия единичной силы, приложенной в точке, для которой ищется перемещение, в направлении искомых перемещений (рис. 6.11) – эпюры 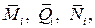а затем вычислить
искомое перемещение по формуле (6.9) с использованием одной из численных формул – по левым, правым или средним прямоугольникам либо по формуле трапеций. При этом обычно переходят от интегрирования по дуге (d s) к интегрированию по горизонтальной ординате (d х), вводя замену (рис. 6.10):

,

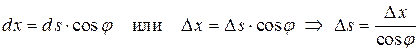с учетом которой выражение (6.9) принимает вид:

или .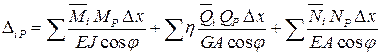

При учете только изгибающих моментов и при постоянной величине жесткости арки выражение для определения перемещений принимает вид:

.

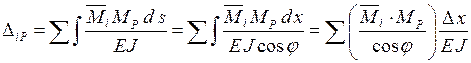Принципы вычисления ординат усилий определяются подходом к численному расчету.

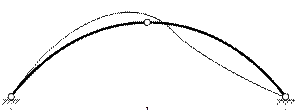
Если вычислить перемещения в
достаточно большом количестве точек,
то можно получить деформированный

вид арки (рис. 6.12).

Date: 2015-05-22; view: 1471; Нарушение авторских прав