
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Геометрические свойства смешанного произведения
|
|
1. Модуль смешанного произведения некомпланарных векторов 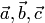 равен объему
равен объему 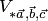 параллелепипеда, построенного на этих векторах. Произведение
параллелепипеда, построенного на этих векторах. Произведение 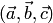 положительно, если тройка векторов
положительно, если тройка векторов 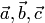 — правая, и отрицательно, если тройка
— правая, и отрицательно, если тройка 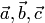 — левая, и наоборот.
— левая, и наоборот.
2. Смешанное произведение 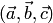 равно нулю тогда и только тогда, когда векторы
равно нулю тогда и только тогда, когда векторы 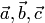 компланарны:
компланарны:
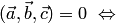 векторы
векторы 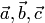 компланарны.
компланарны.
Докажем первое свойство. Найдем по определению смешанное произведение: 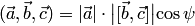 , где
, где 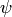 — угол между векторами
— угол между векторами 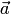 и
и 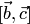 . Модуль векторного произведения (по геометрическому свойству 1) равен площади
. Модуль векторного произведения (по геометрическому свойству 1) равен площади 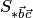 параллелограмма, построенного на векторах
параллелограмма, построенного на векторах 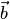 и
и 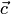 :. Поэтому
:. Поэтому 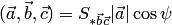 . Алгебраическое значение
. Алгебраическое значение  длины проекции вектора
длины проекции вектора 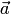 на ось, задаваемую вектором
на ось, задаваемую вектором 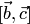 , равно по модулю высоте
, равно по модулю высоте 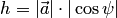 параллелепипеда, построенного на векторах
параллелепипеда, построенного на векторах 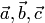 (рис. 1.47). Поэтому модуль смешанного произведения равен объему
(рис. 1.47). Поэтому модуль смешанного произведения равен объему  этого параллелепипеда:
этого параллелепипеда:
Знак смешанного произведения определяется знаком косинуса угла 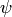 . Если тройка
. Если тройка 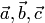 правая, то
правая, то 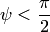 и смешанное произведение
и смешанное произведение 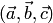 положительно. Если же тройка
положительно. Если же тройка 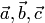 левая, то
левая, то 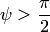 и смешанное произведение
и смешанное произведение 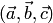 отрицательно.
отрицательно.
Докажем второе свойство. Равенство 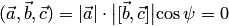 возможно в трех случаях:
возможно в трех случаях:  или
или 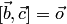 (т.е.
(т.е. 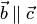 ),или
),или  (т.е. вектор
(т.е. вектор 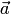 принадлежит плоскости векторов
принадлежит плоскости векторов 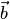 и
и 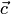 ). В каждом случае векторы
). В каждом случае векторы 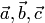 компланарны (см. разд. 1.1).
компланарны (см. разд. 1.1).
 Смешанным произведением трех векторов
Смешанным произведением трех векторов 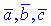 называется число, равное векторному произведению первых двух векторов,
называется число, равное векторному произведению первых двух векторов, 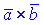 , умноженному скалярно на вектор
, умноженному скалярно на вектор  . Векторами это можно представить так
. Векторами это можно представить так
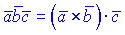 Так как векторы
Так как векторы 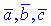 на практике задают в координатной форме, то их смешанный произведение равен определитель, построенном на их координатам
на практике задают в координатной форме, то их смешанный произведение равен определитель, построенном на их координатам 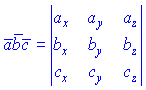 В силу того, что векторное произведение антикомутативно, а скалярное произведение коммутативно, то циклическая перестановка векторов в смешанном произведении не изменяет его значение. Перестановка двух соседних векторов меняет знак на противоположный
В силу того, что векторное произведение антикомутативно, а скалярное произведение коммутативно, то циклическая перестановка векторов в смешанном произведении не изменяет его значение. Перестановка двух соседних векторов меняет знак на противоположный

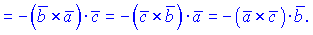
Смешанный произведение векторов положительный, если они образуют правую тройку и отрицательный - если левую.
Геометрические свойства смешанного произведения 1. Объем параллелепипеда, построенного на векторах 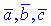 равен модулю смешанного произведения этих век
равен модулю смешанного произведения этих век 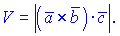 торов. 2. Объем четырехугольной пирамиды равен трети модуля смешанного произведения
торов. 2. Объем четырехугольной пирамиды равен трети модуля смешанного произведения 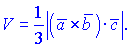 3. Объем треугольной пирамиды равен одной шестой модуля смешанного произведения
3. Объем треугольной пирамиды равен одной шестой модуля смешанного произведения 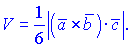 4. Векторы
4. Векторы 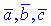 планарных тогда и только тогда, когда
планарных тогда и только тогда, когда 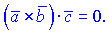 В координатах условие компланарности означает равенство нулю определителя
В координатах условие компланарности означает равенство нулю определителя 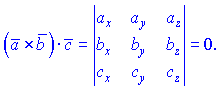 Для практического усвоения рассмотрим примеры. Пример 1.
Для практического усвоения рассмотрим примеры. Пример 1.
Определить, какой тройкой (правой или левой) являются векторы



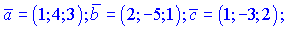
 Решение.
Решение.
Найдем смешанное произведение векторов и по знаку выясним, какую тройку векторов они образуют
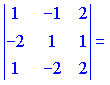
 Векторы образуют правую тройку
Векторы образуют правую тройку 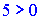
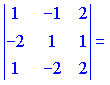
 Векторы образуют правую тройку
Векторы образуют правую тройку 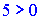
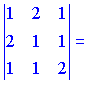
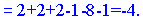 Векторы образуют левую тройку
Векторы образуют левую тройку 
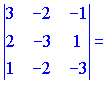
 Векторы образуют правую тройку
Векторы образуют правую тройку 
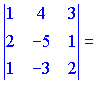
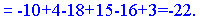 Векторы образуют левую тройку
Векторы образуют левую тройку 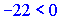
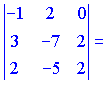
 Данные векторы линейно зависимы.. Смешанным произведением трех векторов. Смешанным произведением трех векторов называется число
Данные векторы линейно зависимы.. Смешанным произведением трех векторов. Смешанным произведением трех векторов называется число

Геометрическое свойство смешанного произведения:
Теорема 10.1. Объём параллелепипеда, построенного на векторах 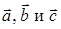 равен модулю смешанного произведения этих векторов
равен модулю смешанного произведения этих векторов
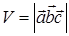 ,
,
или объём тетраэдра (пирамиды), построенного на векторах 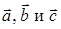 равен одной шестой модуля смешанного произведения
равен одной шестой модуля смешанного произведения
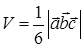 .
.
Доказательство. Из элементарной геометрии известно, что объём параллелепипеда равен произведению высоты на площадь основания
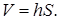
Площадь основания параллелепипеда S равна площади параллелограмма, построенного на векторах 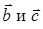 (см. рис. 1). Используя
(см. рис. 1). Используя
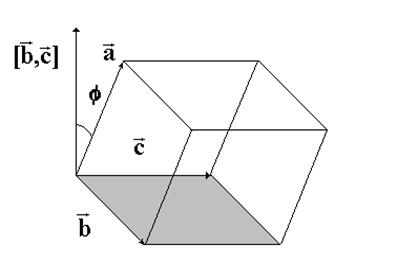 Рис. 1. К доказательству теоремы 1. геометрический смысл векторного произведения векторов
Рис. 1. К доказательству теоремы 1. геометрический смысл векторного произведения векторов 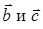 , получаем, что
, получаем, что
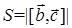 .
.
Далее, если тройка векторов 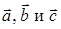 является правой (как на рис. 1), то высота параллелепипеда равна проекции вектора
является правой (как на рис. 1), то высота параллелепипеда равна проекции вектора 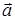 на вектор
на вектор  , т.е.
, т.е.

Отсюда получаем 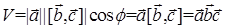 Если тройка векторов
Если тройка векторов 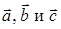 левая, то вектор
левая, то вектор 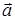 и вектор
и вектор  направлены противоположно, тогда
направлены противоположно, тогда 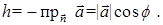 или
или 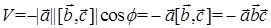 Таким образом, попутно доказано, что знак смешанного произведения определяет ориентацию тройки векторов
Таким образом, попутно доказано, что знак смешанного произведения определяет ориентацию тройки векторов 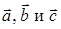
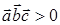 тройка правая и
тройка правая и 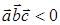 ‑ тройка левая). Докажем теперь вторую часть теоремы. Из рис. 2 очевидно, что объем треугольной призмы, построенной на трех векторах
‑ тройка левая). Докажем теперь вторую часть теоремы. Из рис. 2 очевидно, что объем треугольной призмы, построенной на трех векторах 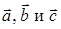 равен половине объема параллелепипеда, построенного на этих векторах, то есть
равен половине объема параллелепипеда, построенного на этих векторах, то есть 
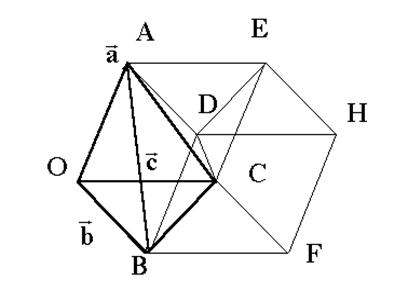 Рис. 2. К доказательству теоремы 1.
Рис. 2. К доказательству теоремы 1.
Но призма состоит из трех одинакового объема пирамид OABC, ABCD и ACDE. Действительно, объемы пирамид ABCD и ACDE равны, так как они имеют равные по площади основания BCD и CDE и одинаковую высоту, опущенную из вершины A. То же справедливо для высот и оснований пирамид OABC и ACDE. Отсюда
Date: 2015-05-22; view: 708; Нарушение авторских прав