Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?
Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника
Координаты точки, радиус- вектор точки, произвольные вектора. Длина вектора
|
|
Сохраняет линейные операции: сумме векторов соответствует сумма их одноименных координат, произведению вектора на число соответствует произведение его координат на это число. Такое взаимно однозначное соответствие называется изоморфизмом.
На практике координаты векторов удобно представлять в виде матриц-столбцов (или матриц-строк), которые называются координатными столбцами (координатными строками).
В базисе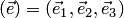 
вектору 
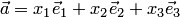соответствует координатный столбец 
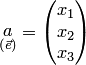.Обозначение базиса 
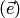можно не указывать, если не может возникнуть неоднозначности. Линейным операциям над векторами соответствуют линейные операции над их координатными столбцами. Например, если в одном и том же базисе 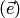векторам 
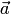и 
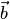соответствуют координатные столбцы 
и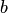 
, то их линейной комбинации 
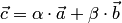соответствует координатный столбец 
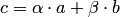, т.е. координатный столбец линейной комбинации векторов равен линейной
Координаты точки, радиус- вектор точки, произвольные вектора. Длина вектора.
Проекция т. М на α Чтобы найти проекцию точки на прямую, нужно через точку провести плоскость перпендикулярно этой прямой.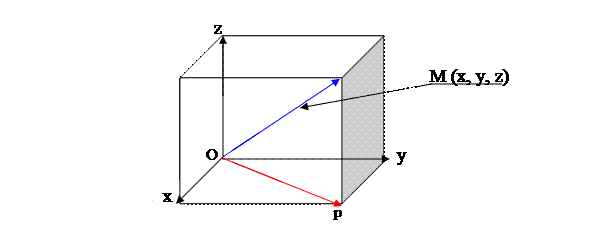 
Опр. Вектор, соединяющий начало координат т. О с произвольной точкой пространства называется радиус- вектор этой точки. Радиус- вектор т. М – ОМ.
Найдем координаты радиус- вектора ОМ
ОА= xi
ОВ= yj
ОС= zk
OM= OP+ PM= OA+ OB+ OC= xi+ yj+ zk= (x, y, z)
Вывод: координаты радиус- вектора точки совпадает с координатами самой точки ОМ= (x, y, z)
Вектор ОМ является диагональю параллелепипеда, по свойству диагоналей d2= a2+ b2+ c2 отсюда следует, что │ОМ│2= x2+ y2+ z2. Извлекая, квадратный корень получаем длину 
Возьмем две произвольные точки. т. А(x1, y1, z1) и т. В (x2, y2, z2). Соединим АВ.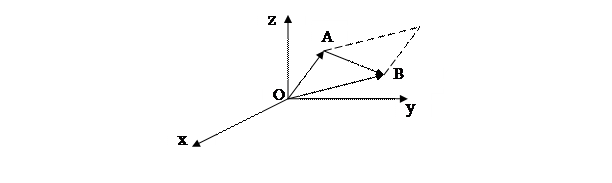 
Вспомогательные векторы
ОА= (x1, y1, z1)
ОВ= (x2, y2, z2)
АВ= ОВ- ОА= (x2, y2, z2)- (x1, y1, z1)= (x2- x1,, y2- y1, z2- z1)
Вывод: чтобы найти координаты вектора нужно их координат конца вектора вычесть соответствующие координаты начала вектора.
АВ= (x2- x1,, y2- y1, z2- z1)
Пр. Даны 3 точки. т. А(2,-1,3), т. В(4,0,1), т. С(-1,2,1). Найти АВ и его длину │АВ│, m= AB- 2BC.
Date: 2015-05-22; view: 702; Нарушение авторских прав