Условия параллельности и перпендикулярности прямых

Определение 1. Уравнением линии на плоскости O xy называется уравнение F (x, y)=0, которому удовлетворяют координаты x и y каждой точки линии и только они.

Если из этого уравнения выразить переменную y, то получится уравнение y = f (x).

Если линии заданы уравнениями, то точкой пересечения двух линий называется любая точка, координаты x и y которой удовлетворяют уравнениям, т.е. являются решением системы двух уравнений.

Основные виды уравнений прямой на плоскости:

1) у =0 - уравнение оси О х; y = b - уравнение прямой, параллельной оси О х;

2) х =0 - уравнение оси О у; х = а - уравнение прямой, параллельной оси О у;

3) y = kх - уравнение прямой, проходящей через начало координат, с угловым коэффициентом k =tga, где a- угол наклона прямой к оси O х;

4) y = kх+b - уравнение прямой с угловым коэффициентом k =tga, где a- угол наклона прямой с положительным направлением оси O х.

y - y ₀= k (x - x ₀) - уравнение прямой, проходящей через точку (x ₀, y ₀) и имеющей угловой коэффициент k.

уравнение прямой, проходящей через две данные точки (x ₁, y ₁) и (x ₂, y ₂), если x ₁¹ x ₂ и y ₁¹ y ₂.

Определение 1. Уравнение с двумя переменными Ax + By + C = 0, где A и B не равны 0 одновременно, называется общим уравнением прямой на плоскости.

Теорема 1. Любая прямая на плоскости может быть задана общим уравнением.

Если В¹0, то

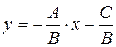т.е. y = кх+b. При этом: а) если А=0, то y = b;

б) если А=0 и С=0, то y =0;

в) если С=0, то y = кх.

Если В=0 и А¹0, то 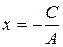, т.е. х = а - если С¹0 и х =0 - если С=0.

Теорема доказана.

Точка пересечения двух прямых A ₁ x + B ₁ y + C ₁ = 0и A ₂ x + B ₂ y + C ₂ = 0есть решение системы линейных уравнений

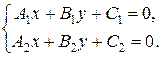
Пусть две прямые заданы уравнениями с угловыми коэффициентами y = к ₁ х+b ₁ и y = к ₂ х+b ₂, т.е. k ₁=tga₁ и k ₂=tga₂, где a₁ и a₂ - углы наклона прямых к оси О х.

Рассмотрим угол j=a₂-a₁ - угол между данными прямыми. Тогда, по формуле тангенса разности, 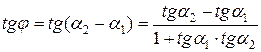, т.е. .

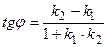Если прямые параллельны, то j = 0, tgj = 0.

Итак, условием параллельности двух прямых является равенство их угловых коэффициентов, т.е. k ₁= k ₂.

Если прямые перпендикулярны, то j = p/2, ctgj = 0.

Итак, условием перпендикулярности двух прямых является равенство k ₁× k ₂ =-1.

Замечание. Можно показать, что если две прямые заданы общими уравнениями A ₁ x + B ₁ y + C ₁ = 0и A ₂ x + B ₂ y + C ₂ = 0, то:

условие параллельности прямых: ;

условие перпендикулярности прямых: A ₁ A ₂ + B ₁ B ₂ = 0.