Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?
Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника
I. Элементы линейной алгебры и аналитической геометрии
|
|
Пример 1. Даны векторы 
1(2; 4; 3; 2), 2(4; 2; 2; 8), 3(4; 5; 8; 7), 4(6; 7; 5; 3) и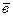 
(18; 24; 13; 6). Показать, что векторы 
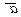1, 2, 3, 4 образуют базис четырехмерного линейного пространства R4 и найти координаты вектора 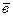в этом базисе.
Решение.
Выражение х1+ 1+х2 2+…+хк к называется линейной комбинацией векторов 1, 2, … к с коэффициентами х1, х2, …хк. Любая линейная комбинация векторов линейного пространства представляет собой вектор того же пространства. Если некоторый вектор 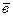линейного пространства представлен в виде линейной комбинации векторов 1,…, к того же пространства, т.е.
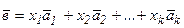(1)
то говорят, что вектор 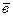разложен по векторам 1,… к Система векторов 1, 2, … к некоторого линейного пространства называется линейно независимым, если равенство
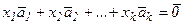(2)
имеет место только при нулевых значениях коэффициентов х1, х2, …, хк, если же равенство (2) выполняется и при условии, что хотя бы один из коэффициентов х1, х2, …, хк, отличен от нуля, то система векторов 1, 2, … к называется линейно зависимой.
Для векторов с заданными координатами 1(х1, y1, z1, p1), 2(x2, y2, z2, p2), 3(x3, y3, z3, p3), 4(x4, y4, z4, p4), составим определитель и вычислим его.
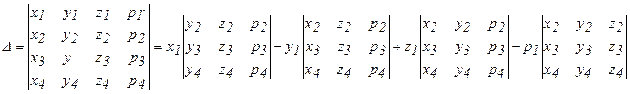(3)
Date: 2015-04-23; view: 706; Нарушение авторских прав